-
Пожалуйста решитеУмоляю!!!! Ответ: 30
Задача по геометрии. Если не можете, не пишите не могу и получили баллы. Не издевайтесь, ведь мне действительно нужно решение этой задачи.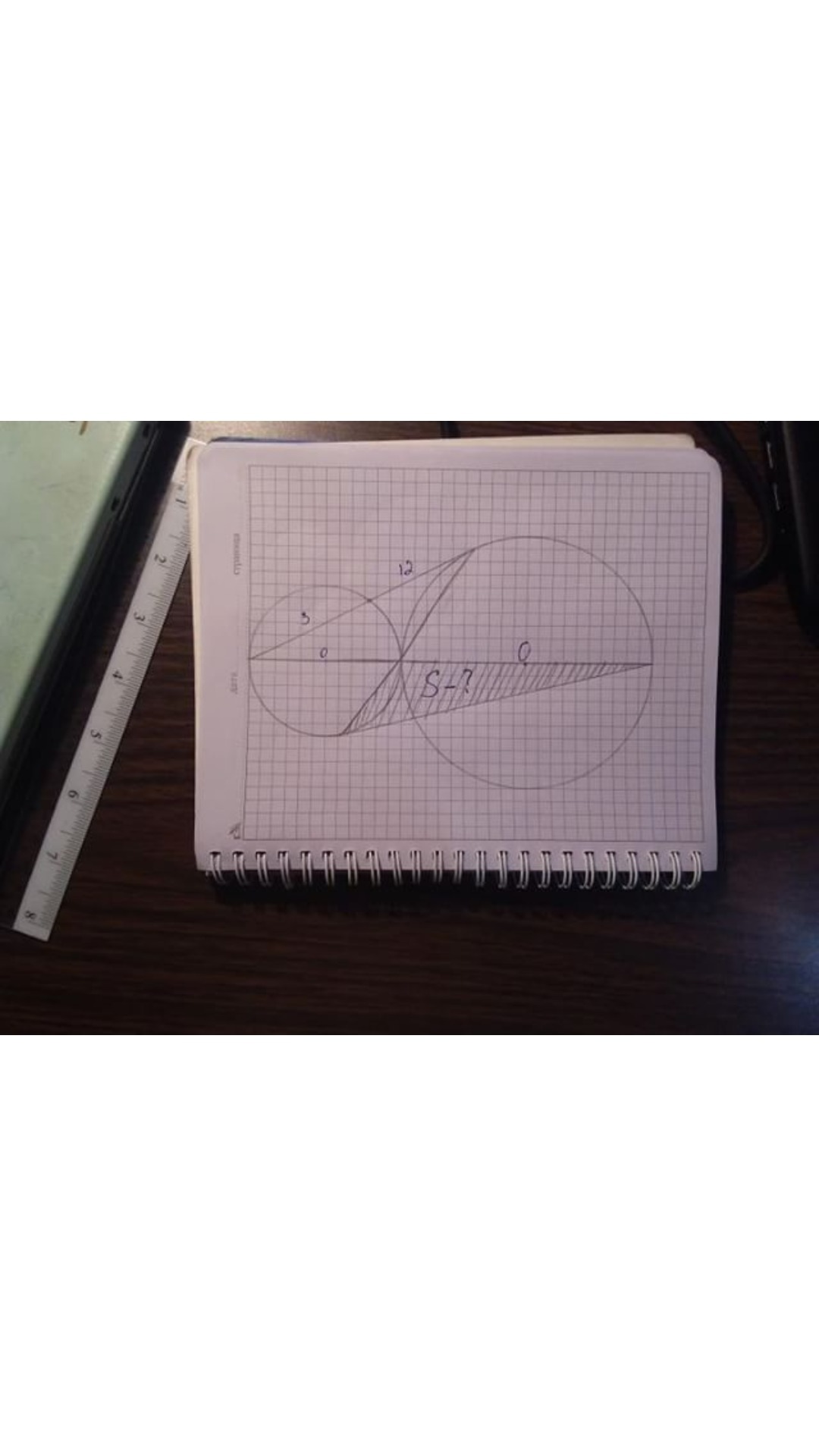
-
Предмет:
Геометрия -
Автор:
zayneraymond - 6 лет назад
-
Ответы 1
-
--- 1 ---на рисунке 1 маленький жёлтый треугольник подобен большому синемут.к. один угол общий, второй прямойr/1.5 = (2r + R)/(12 + 3)r/1.5 = (2r + R)/1510r = 2r + RR = 8r--- 2 ---Теорема Пифагора для большого синего треугольника15² + R² = (2r + R)²15² + (8r)² = (2r + 8r)²15² + 64r² = 100r²15² = 36r²5² = 4r²r² = (5/2)²r = 5/2R = 8r = 20 --- 3 ---рисунок 2Синий и красный треугольники подобны - оба они равнобедренные, и углы при основаниях равны как вертикальные--- 4 ---угол при вершине β можно найти из большого прямоугольного треугольника со сторонами 15, 20 и 2r + R = 2*2.5 + 20 = 25sin(β) = 15/25 = 3/5--- 5 ---Высота красного треугольника, проведённая к боковой сторонеh = 2.5*sin(β) = 2.5*3/5 = 7.5/5 = 1.5--- 6 ---Основание искомого треугольника 2R = 40Высота равна высоте маленького красного на рис 2h = 1.5ПлощадьS = 1/2*40*1.5 = 20*1.5 = 30------ПримечаниеНа картинке кажется, что изображены касательные к двум окружностям, и к маленькой и к большой. Но для циферок в 3 и 12 такое невозможно. В итоге касательная только одна, к большой окружности.

-
Автор:
patricio - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
В 135 г воды растворили 15 г соли. Ка кова массовая доля растворенного вещества в растворе
-
Предмет:
Химия -
Автор:
osvaldoallison - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
1. а)Найдите сумму целых чисел, расположенных между числами -8 и 11
б) Произведение целых чисел, расположенных между числами -9 и 100
в) Найдите сумму натуральных чисел, расположенных числами -124 и 3
г) Найдите сумму натуральных чисел, расположенных между числами -5 и 1092
-
Предмет:
Математика -
Автор:
damián74 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Шар пересечен плоскостью, отстоящей от центра на расстоянии 5 см. Найдите радиус шара, если радиус сечения равен 12 см.
-
Предмет:
Математика -
Автор:
coleman2 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Закончите предложения, используя слова, данные справа:
1. the intense heat is … by the arc.
2. the electric arc is the best … of
the heat energy.
3. the arc is able to melt … metals.
4. sometimes the arc is … between the two non-consumable electrodes.
5. there are two types of current … and …
6. the depth of fusion is named … .
7. the electrode … is used for holding an electrode.
8. when the electrode is in contact with the work, the … is completed.
9. the electric current and polarity, both … and … are an important factor in producing high quality welds.
10. the ... cables connect the … metal with a … of energy.
11. the … electrode is a conductor and at the same time a … metal.
12. intense heating … in melting the base metal and the electrode. Penetration
Circuit
Ground
To be created
Filler
To result (in)
Alternating
Source
To be produced
Reverse
Holder
Straight
Direct
Base
Refractory
Consumable
Quality
Property-
Предмет:
Английский язык -
Автор:
maya95 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
