-
а) Докажи,что ABCD- параллелограмм и PO=HO
б) Докажи,что треугольник POA= треугольник HOB и PA=HB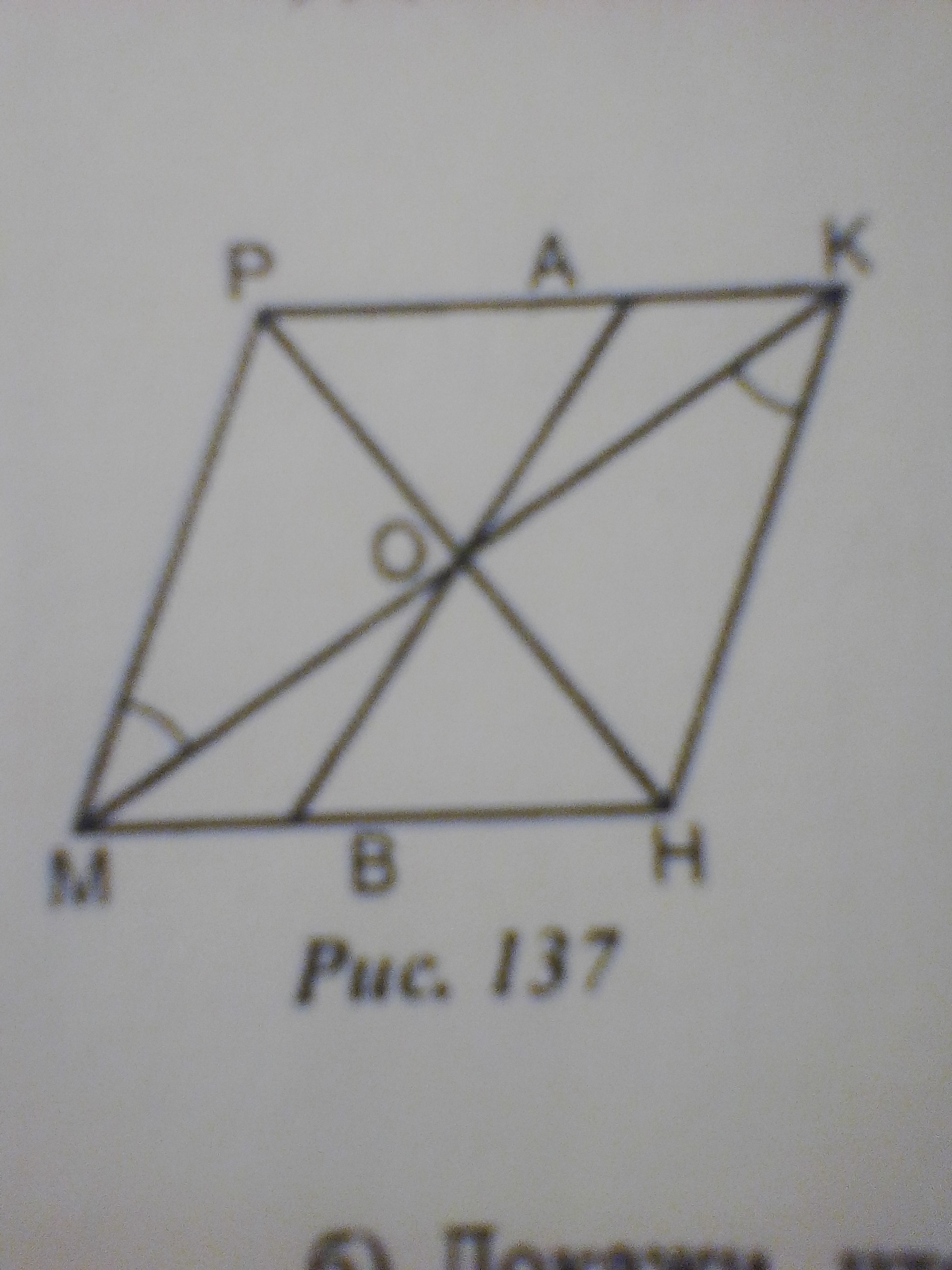
Ответы 1
-
1. Признак: "Если в четырехугольнике две противоположные стороны равны и параллельны, то этот четырехугольник — параллелограмм".
Стороны АВ=СD (дано). Углы ВАС и АСD равны (дано). Это накрест лежащие углы при прямых АВ и CD и секущей АС. Следовательно, эти прямые параллельны (признак). АВСD - параллелограмм по приведенному выше признаку. Что и требовалось доказать.
2. Треугольники ADB и DCB равны по двум углам (<1=<4 и <2=<3 - дано) и стороне между ними - DB - общая. В равных треугольниках против равных углов лежат равные стороны.
AD=CB, DC=AB. ABCD - параллелограмм по признаку: "Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник — параллелограмм".
Что и требовалось доказать.
-
Автор:
cookiecubq - 6 лет назад
-
0
-
-
Добавить свой ответ
-
сочинение на тему "ранее утро" 4-5предложений
-
Предмет:
Русский язык -
Автор:
joey22 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите решить!!!!!! Умоляю пожалуйста!!!!!! Учительница злая, завтра проверяет
-
Предмет:
Английский язык -
Автор:
alisson1hy6 - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
ПОМОГИТЕ ПОЖАЛУЙСТА <3
Make up 8 sentences that are true for you using the sports vocabulary from previous exercises and time expressions always/never/all (year, my life) or since/for.
For example: I have never tried professional sports in my life, because it requires so much stamina. I have been only doing some amateur sports all the time.-
Предмет:
Английский язык -
Автор:
stella81 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помогите пожалуйста нам задали традиции нашей семьи какие у вас традиции
-
Предмет:
Литература -
Автор:
haas - 6 лет назад
-
Ответов:
1 -
Смотреть
-
