Пожалуйста помогите!
Срочно!
Первому лучший ответ!

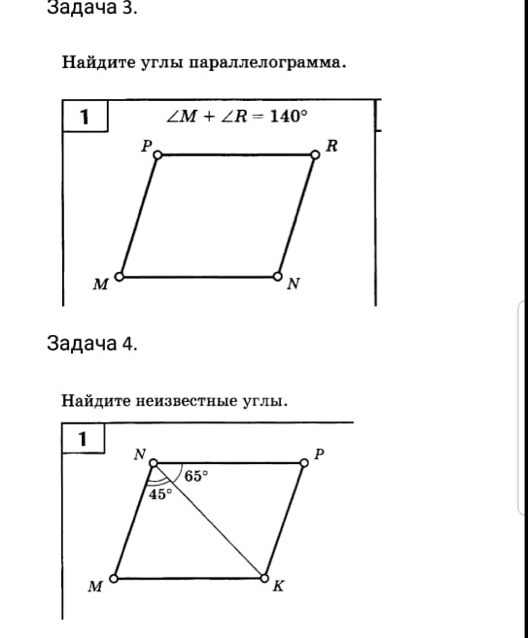
задача #1РЕШЕНИЕ:1)т.к MPRN- параллелограмм, значит <M=<R по 1 свойству параллелограмма 2)т.к <M+<R=140, <M и <R= 140:2=70°3)т.к MPRN-параллелограмм, значит <P=<N по 1 свойству параллелограмма 4)<P и <N= (360-<M-<R):2= (360-70-70):2=110°ОТВЕТ: <M=70°, <P=110°, <R=70°, <N=110°задача #2РЕШЕНИЕ:1)т.к MNPK-параллеограм, то MN||PK по определению параллелограмма 2)<MNK=<NKP=45°<PNK=NKM=65° при MN||PK и секущей NK.3)<K и <N= 65+45=110°4)т.к MNPK- параллелограмм, то <M=<P по 1° параллелограмма5)<M и <P= (360-<N-<K):2=(360-110-110):2=70°ОТВЕТ: <M=70°, <N=110° , <P= 70°, <K= 110°.