-
Найдите угол между плоскостью MKL и прямой MB в правильной четырехугольной пирамиде, все ребра которой равны (см. рисунок)
P. S. Поподробнее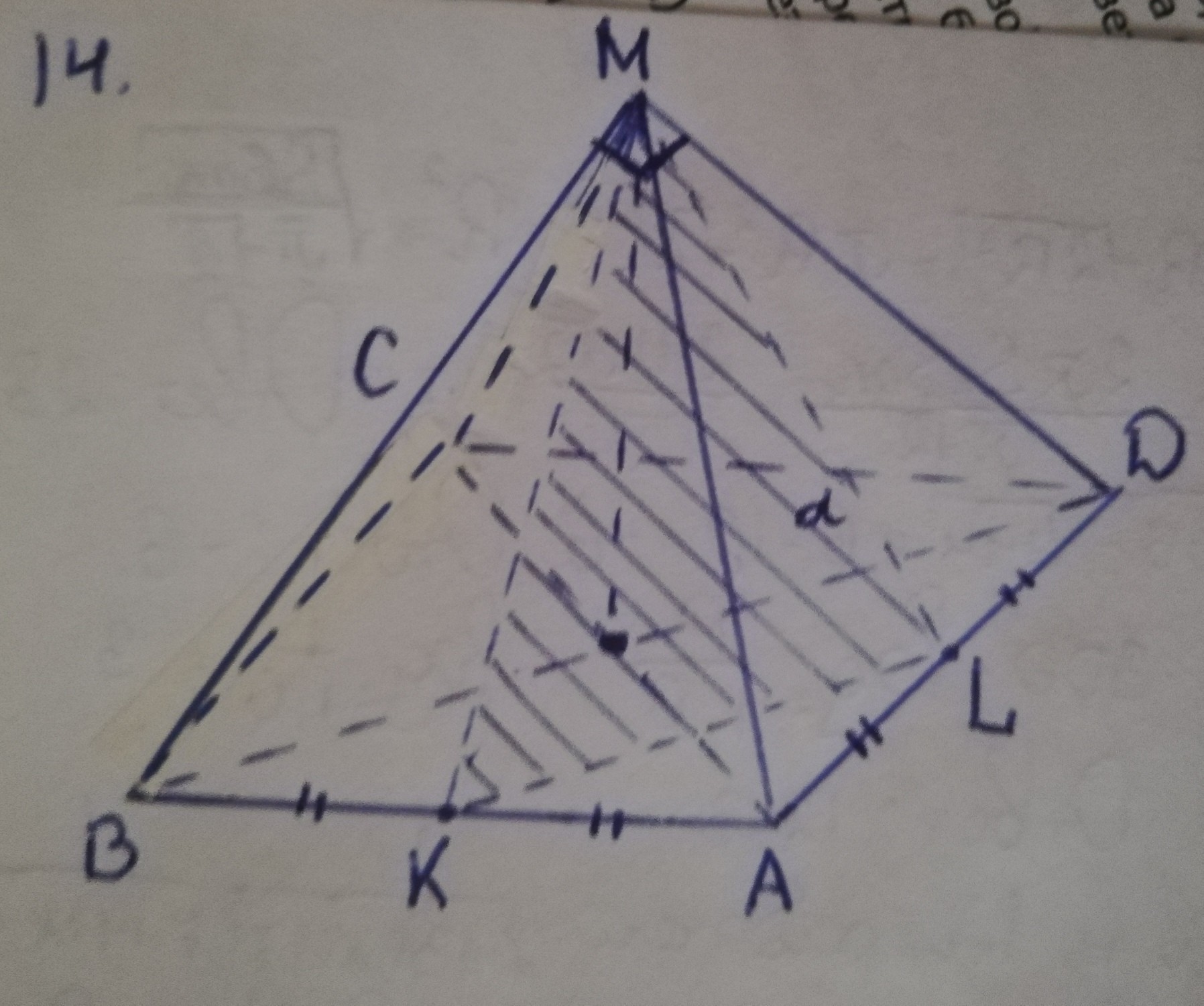
Ответы 7
-
или дайте теорию прочитать где нибудь про это
-
Автор:
hawkf1mv - 6 лет назад
-
0
-
-
Это нарисовал он левую ) - не важно. Ошибки я не вижу ...
-
Автор:
shannon - 6 лет назад
-
0
-
-
Ну отмечай. Есть кому проверить...
-
Автор:
allieguzman - 6 лет назад
-
0
-
-
ок
-
Автор:
twiggy94wx - 6 лет назад
-
0
-
-
я тоже не нашла ошибки (уравнение плоскости составляла через смеш. произведение).
-
Автор:
creepbljt - 6 лет назад
-
0
-
-
Пусть A - начало координат
Ось X - AB
Ось Y - AD
Ось Z - вверх от ABC в сторону M
Пусть Все ребра единичные.
O- Центр пересечения диагоналей ABCD
Из Треугольника AOM -
AO = MO = √2/2
Координаты точек
M (0,5 ; 0,5 ;√2/2)
K (0,5 ; 0 ; 0)
L (0 ; 0.5 ; 0 )
Вектор MB ( 0,5 ; -0,5 ; - √2/2)
Уравнение плоскости MKL
ax+by+cz+d=0
Подставляем координаты принадлежащих плоскости точек
0,5 a + 0,5 b + √2/2 c + d =0
0,5 a + d =0
0,5 b + d = 0
Пусть d = -1 Тогда a =2 b =2 c= - √2
Уравнение
2x+2y-√2z-1 =0
Нормаль n(2; 2; -√2)
Cинус искомого Угла
| n * MB | / | n | / | MB | = | 1 - 1 + 1 | / √(4+4+2) / √{1/4+1/4+1/2) = 1 / √10
-
Автор:
crumbles - 6 лет назад
-
0
-
-
Искомый угол - <ВМP. ВP=OH - расстояние от прямой BD до плоскости MKL (высота из прямого угла MOQ). Тогда PM - проекция BM на плоскость MKL. МO=BO = a√2/2. OQ=a√2/4. MQ=√(2a²/4+2a²/16) = a√10/4. ОН=BP=MO*OQ/MQ = a/√10.
Sinα = BP/BM = (a/√10)/a = 1/√10
Или подробнее:
Точки В и О лежат на прямой, включающей в себя диагональ BD квадрата АВСD. Плоскость KML включает в себя равнобедренный треугольник KML, высота которого МQ лежит на линии пересечения взаимно перпендикулярных плоскостей KML и AMC (диагонали квадрата АВСD взаимно перпендикулярны). Расстояние от точки О до плоскости MKL это перпендмкуляр ОН к прямой MQ, то есть это высота из прямого угла треугольника OMQ. Заметим, что треугольник МОВ - равнобедренный (BD=a√2, BO=a√2/2, а так как все ребра пирамиды равны, то в треугольнике ВОМ катет МО=a√2/2). МO=BO =a√2/2. OQ=a√2/4 (половина и четверть диагонали квадрата - основания пирамиды соответственно). Тогда по Пифагору MQ=√(2a²/4+2a²/16)= a√10/4.
По свойству высоты из прямого угла имеем: ОН=MO*OQ/MQ = a/√10.
Проведем через точку Н прямую "а" параллельно диагонали BD (и, соответственно, прямой KL) и опустим перпендикуляр ВР на эту прямую. ВР=ОН, так как ВРНО - прямоугольник (<HOB=<HPB=90°). Проведем прямую MP. Эта прямая лежит в плоскости, включающей в себя треугольник MKL, так как прямая РН и точка М принадлежат этой плоскости. Значит она является проекцией наклонной МВ на эту плоскость (ВР=ОН - перпендикуляры к этой плоскости). Искомый угол между прямой МВ и плоскостью, включающей в себя треугольник MKL, это угол BMP между наклонной МВ и ее проекцией МР на эту плоскость.
Sinα = BP/BM = (a/√10)/a =1/√10 ≈ 0,316.
α = arcsin(0,316) ≈ 18,4° Это ответ.

-
Автор:
chazcowa - 6 лет назад
-
0
-
-
Добавить свой ответ
- Некоторое тело движется равномерно из точки с кординатой 100 м в направлении, противоположном оси ОХ со скоростью 5 м/с . Запишите закон движения тела
-
(34 дм2 + 56 дм2) : 3 = (62 м2- 53м2) ∙ 4 =
-
Предмет:
Математика -
Автор:
probocortez - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
срочно помогите пж контролка по русскому на тему словосочетание
-
Предмет:
Русский язык -
Автор:
bernardq60f - 6 лет назад
-
Ответов:
4 -
Смотреть
-
- СРОЧНО!!!! напишите + и - червей
