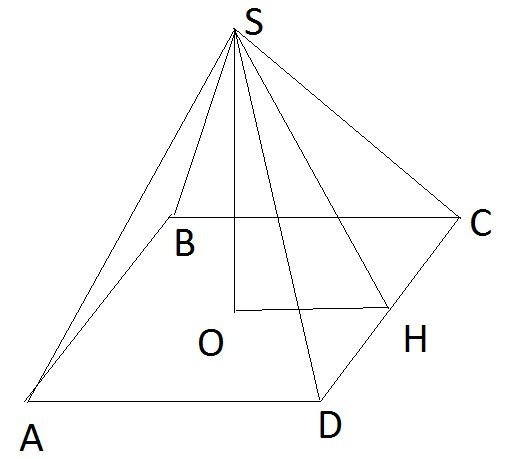
Боковые грани SAB и SCD правильной четырехугольной пирамиды SABCD образуют двугранный угол 60°. Ребро основания АВ равно 1. Найти площадь полной поверхности пирамиды.

Если противолежащие боковые грани образуют двугранный угол 60°, то угол между апофемами этих граней 60°. Поэтому апофемы А равны стороне основания, то есть 1 (образуют равносторонний треугольник).

Периметр основания Р = 4*1 = 4.

Площадь боковой поверхности Sбок = (1/2)РА = (1/2)*4*1 = 2 кв.ед.

Площадь основания So = a² = 1² = 1 кв.ед.

Площадь полной поверхности пирамиды равна:

S = Sбок + Sо = 2 + 1 = 3 кв.ед.