-
Написать уравнения касательных, проведенных из точки A( 10/3, 5/3) к эллипсу x²/20+y²/5=1
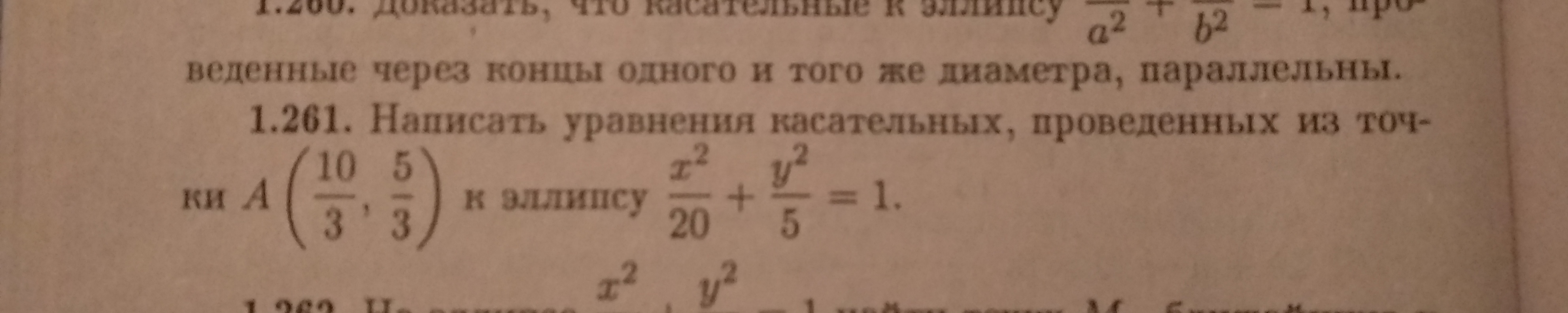
Ответы 1
-
Выразим уравнение эллипса x²/20+y²/5=1 относительно у.
у =+-(1/2)*√(20 - х²). То есть получаем 2 уравнения - они выражают верхнюю и нижнюю половины графика относительно оси Ох.
Производная функции равна:
верх y' = -х/(2√(20 - х²)),
низ y' = х/(2√(20 - х²)).
Получаем 2 уравнения касательных (точка касания (хо; уо)):
у = (1/2)*√(20 - хо²) - х/(2√(20 - х²))*(х - хо). (1)
у = -(1/2)*√(20 - хо²) + х/(2√(20 - х²))*(х - хо). (2)
Известно, что уравнение касательной к эллипсу имеет вид:
(ххо/а²) + (ууо/в²) = 1. (3)
Так как касательная проходит через точку А, подставим её координаты в уравнение (3).
(10*хо/(3*20)) + (5*уо/(3*5)) = 1,
10хо + 20уо = 60.
Получаем хо + 2уо = 6 или
хо = 6 - 2уо. (4)
Подставив хо их уравнения (4) в уравнения (1) и (2), получим уравнения касательных:
у = -х + 5,
у = -х + 2,5.

-
Автор:
sandycherry - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Что такое патриотизм ? Кого называют патриотом? Приведите примеры из жизни?
-
Предмет:
Обществознание -
Автор:
beckwyzw - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
переведите целые числа из десятичной системы счисления в восьмеричную :
а) 513
б) 600
в) 2010
запишите решение-
Предмет:
Информатика -
Автор:
rishif5eo - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
примери 3 4 деоритизм, жергон, и профисиолизм
-
Предмет:
Русский язык -
Автор:
joeyt9wp - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Где впервые разделили земные сутки на двадцать четыре часа?
-
Предмет:
Окружающий мир -
Автор:
bennettbaldwin - 6 лет назад
-
Ответов:
1 -
Смотреть
-
