-
На рисунке NP = PK и NT = TK. Докажите, что
а)треугольник PNT = треугольнику PKT
б)РТ - биссектриса угла Р
в) NK - перпендикулярен РТ
Дано :......
Доказать:.......
Док-во:......
пожалуйста, помогите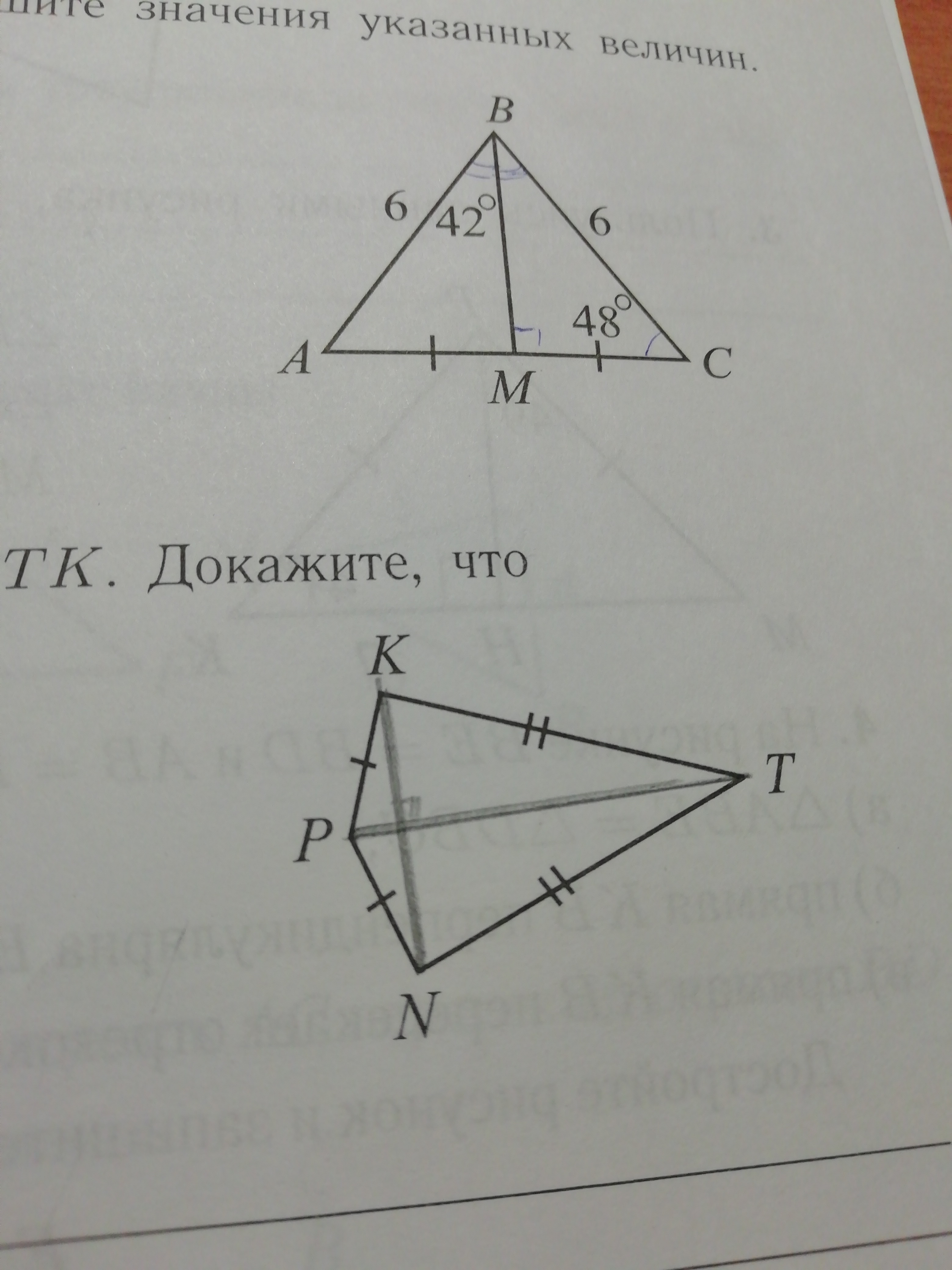
Ответы 1
-
Дано:
Выпуклый 4х-угольник PKTN
PN=PK, TK=TN
Доказать:
1) ΔPNT=ΔPKT
2) PT - биссектриса ∠P
3)NK⊥PT
Док-во:
1) Рассмотрим ΔPNT и ΔPKT:
- PK=PN (по условию)
- TK=TN (по условию)
- PT - общая сторона
Из этого всего следует, что ΔΔ= по 3 сторонам.
Ч.Т.Д.
2) Т.к. ΔPNT=ΔPKT, то ∠NPT=∠KPT (если ΔΔ=, то = их соответствующие элементы). Следовательно, PT является биссектрисой ∠P.
Ч.Т.Д.
3) Пусть точка пересечения NK и PT будет названа О.
Т.к. ΔPNT=ΔPKT, то ∠NOP=∠KOP (если ΔΔ=, то = их соответствующие элементы), а т.к. ∠NOP и ∠KOT; ∠KOP и ∠NOT вертикальные, то получается: ∠NOP=∠KOT=∠KOP=∠NOT. Сумма этих углов = 360°, поэтому каждый угол будет=360°:4=90°.
Ч.Т.Д.
-
Автор:
dulce88 - 6 лет назад
-
0
-
Добавить свой ответ
Еще вопросы
-
Тест 6 вариант 4 7класс
1)Какое из выражений может быть составлено для вычисления периметра закрашенной фигуры?
Дальше фото. -
СРОЧНО .как образовано слово нависшие???
-
Предмет:
Русский язык -
Автор:
nievesterry - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
сачыненне на тэму пераказ зместу кінафільма
-
Предмет:
Беларуская мова -
Автор:
mikeymacias - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
назвіть головних героїв поеми Іліада
-
Предмет:
Литература -
Автор:
bruceclarke - 6 лет назад
-
Ответов:
3 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
