Помогите с заданием,геометрия 8 класс
задание 24,25

Ответ:

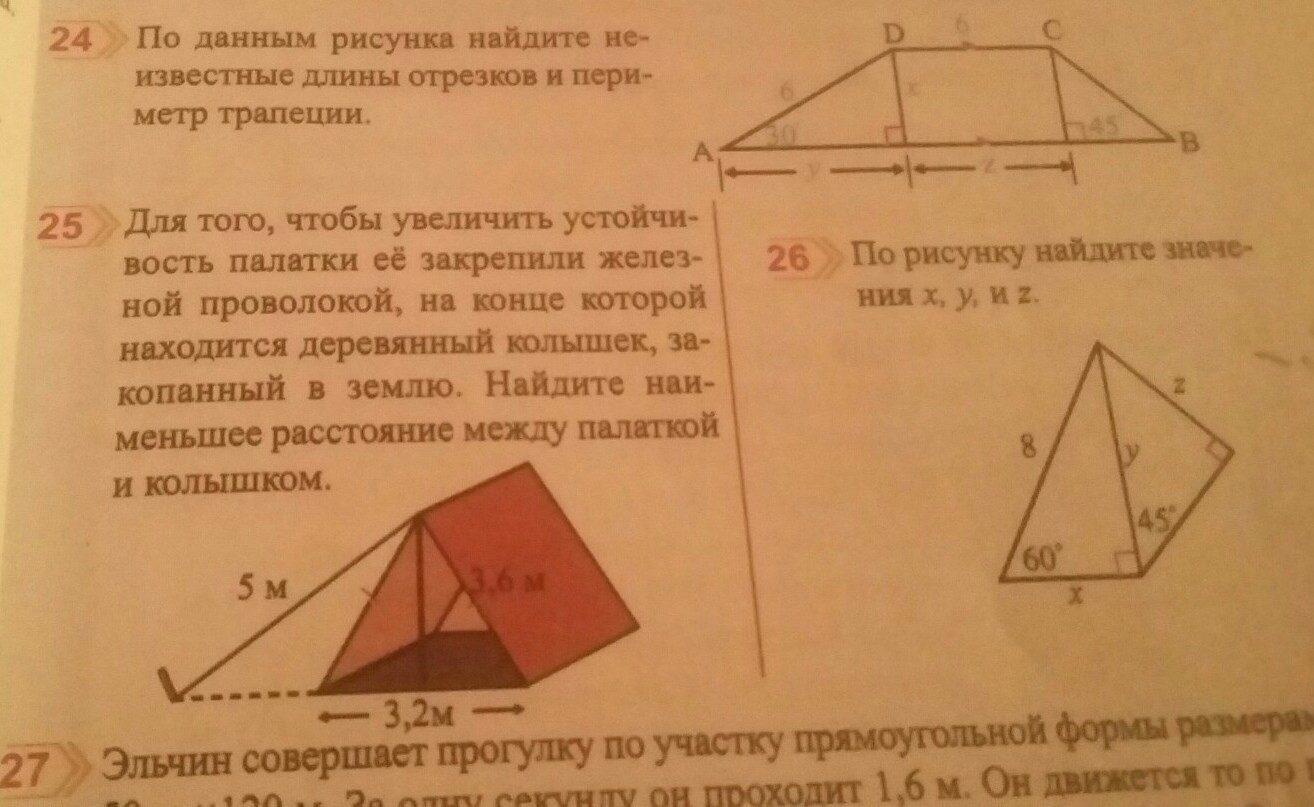
24 задание

y= 3√3

x= 3

z= 6

P≈ 30,44

25 задание

S =1,87 м

Решение:

24 задача

Рассмотрим треугольник ADE

Исходя из свойства треугольника - катет, лежащий против острого угла в 30° (и соответственно, прилежащий к углу в 60°), равен половине гипотенузы. Значит:

x = AD/2

x=6/2=3

По теореме пифагора:

AD²=x²+y²

y²=AD²-x²

y²=36-9

y²=27

y=√27=3√3

Известно, что многоугольник ADCB - трапеция, значит DC║AB ⇒ z =DC = 6.

Так как ∠ADE=∠CFB=90° и DC║AB, а треугольник CBF равнобедренный ⇒ x=CF=BF=3

Найдем CB:

CB²=CF²+FB²

CB²=3²+3²

CB²=9+9=18

CB=√18=3√2

Найдем периметр трапеции:

P=AD+DC+CB+BF+z+y

P=6+6+3√2+3+6+3√3≈30,44

Задача 25

Рассмотрим треугольник ABC.

AB = 5 м

BC = 3,6 м

Найдем AC:

AC² = AB²-BC²

AC² = 5²-3,6²

AC²=12,04

AC=√12,04=3,47

S = AC-3,2÷2=3,47-1,6=1,87 м - наименьшее расстояние

Задание 24

1) x = AD*sin30 = 6*0.5 = 3 - ответ

2) y = AD*cos30 = 6* √3/2 = 3√3 - ответ

3) z = CD = 6 - ответ

4)  BC = x*√2 = 3√2 -  боковая сторона и часть основания.

5) АВ = 3√3 + 6 + 3 = 9+3√3 - нижнее (большое) основание.

6) Р = AB+BC+CD+DA = (9+3√3)+3√2+6+6 = 21+3*(√3+√2) - ответ

Задание 25.

Рисунок к задаче в приложении.

Вспоминаем теорему Пифагора.

Катет в основании - а = 3,2 : 2 = 1,6 - равнобедренный треугольник.

Высота - катет - b - вычисляем b² = 3,6²-1,6² = 12.96-2.56 = 10.4

Вычисляем катет - L = √(5² - 10.4) = √14.6 = 3.82 м - до центра палатки

X= L-1.6 =  3,82 - 1,6 = 2,22 - расстояние до палатки. - ответ