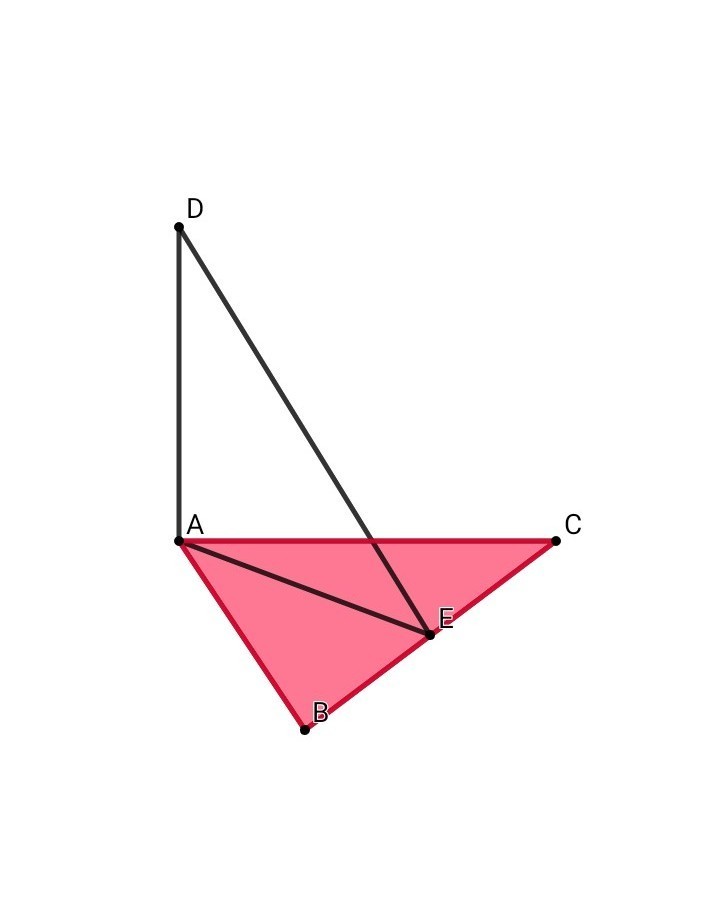
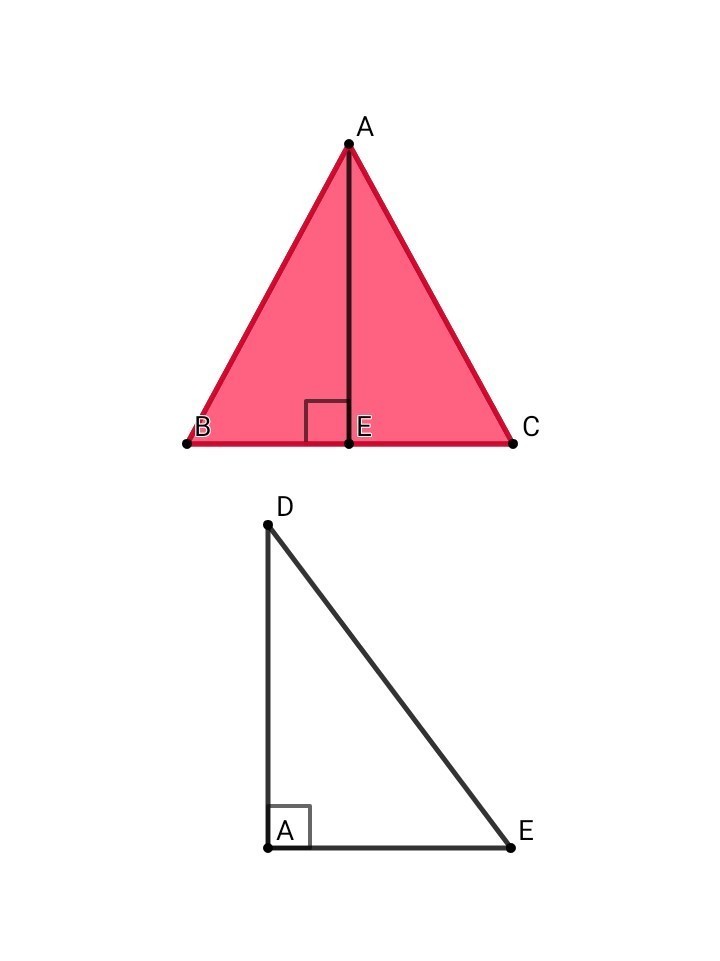
к плоскости равностороннего треугольника ABC проведен перпендикуляр AD,точка E-середина стороны BC.
1)Докажите,что DE⊥BC.
2)Найдите DE,если AB=4 см,AD=3 см

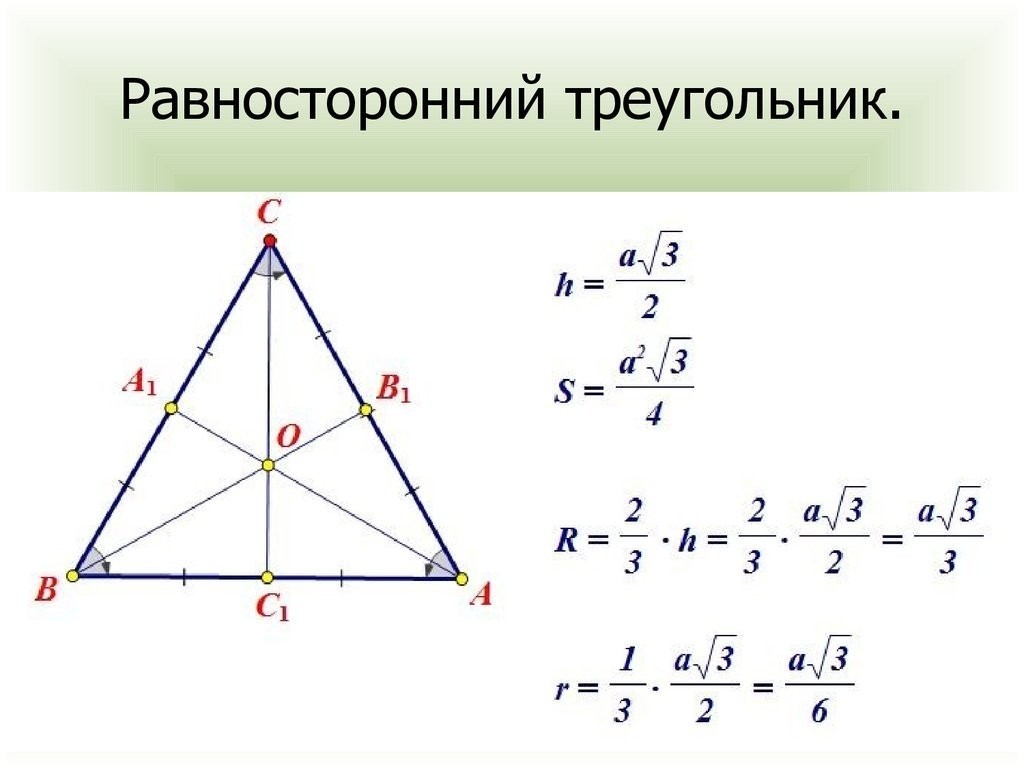
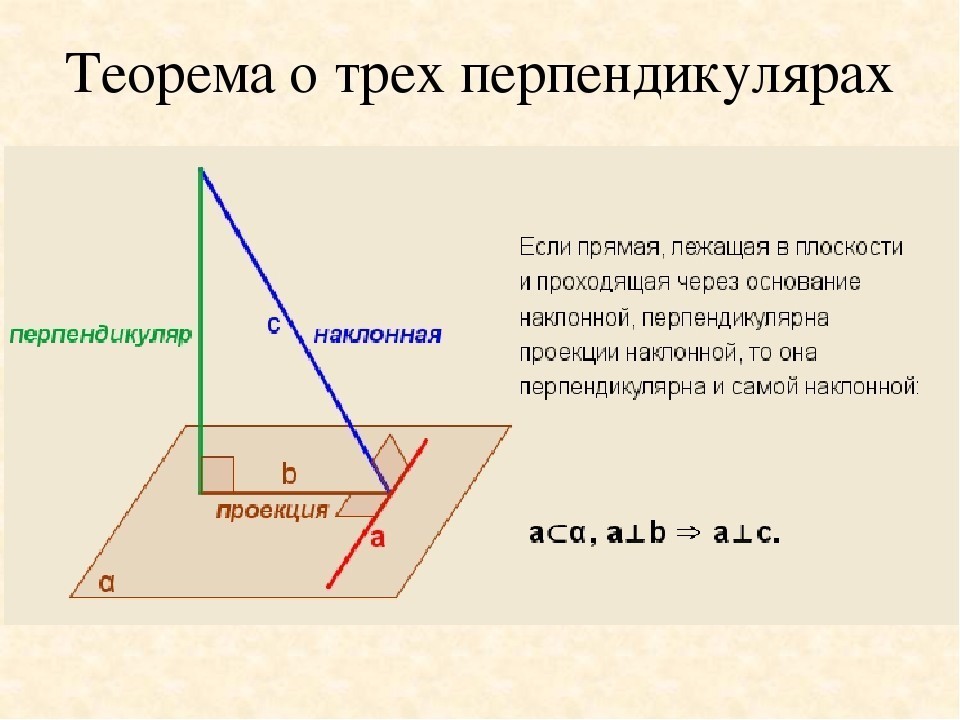
К плоскости равностороннего треугольника ABC проведён перпендикуляр AD, точка E - середина стороны BC.1) Докажите,что DE⊥BC.2) Найдите DE, если AB = 4 см, AD = 3 см.1) Доказательство:▪DA - перпендикуляр к плоскости АВСАЕ - перпендикулярен ВС ( В равностороннем треугольнике любая медиана является и высотой, и биссектрисой )Значит, по теореме о трёх перпендикулярах DE перпендикулярен ВС, что и требовалось доказать.*** см. приложение ***2) Решение:▪ Рассмотрим тр. АВС:Высота в равностороннем треугольнике рассчитывается через сторону по формуле:h = a•V3 / 2 => AE = ABV3/2 = 4V3/2 = 2V3 см ( см. приложение )▪ИЛИ рассмотрев прям. тр. АВЕ:ВЕ = ЕС = ВС/2 = 4 / 2 = 2 смПо теореме Пифагора:АВ^2 = АЕ^2 + ВЕ^2АЕ^2 = 4^2 - 2^2 = 16 - 4 = 12АЕ = V12 = V( 4 • 3 ) = 2V3 см▪Рассмотрим прям. тр. DAE: по т. ПифагораDE^2 = АD^2 + AE^2DE^2 = 3^2 + ( V12 )^2 = 9 + 12 = 21DE = V21 см☆ ОТВЕТ: 1) доказано ; 2) V21 см ☆