решите пожалуйста. надо срочно

спасибо

спасибо

♥♥♥

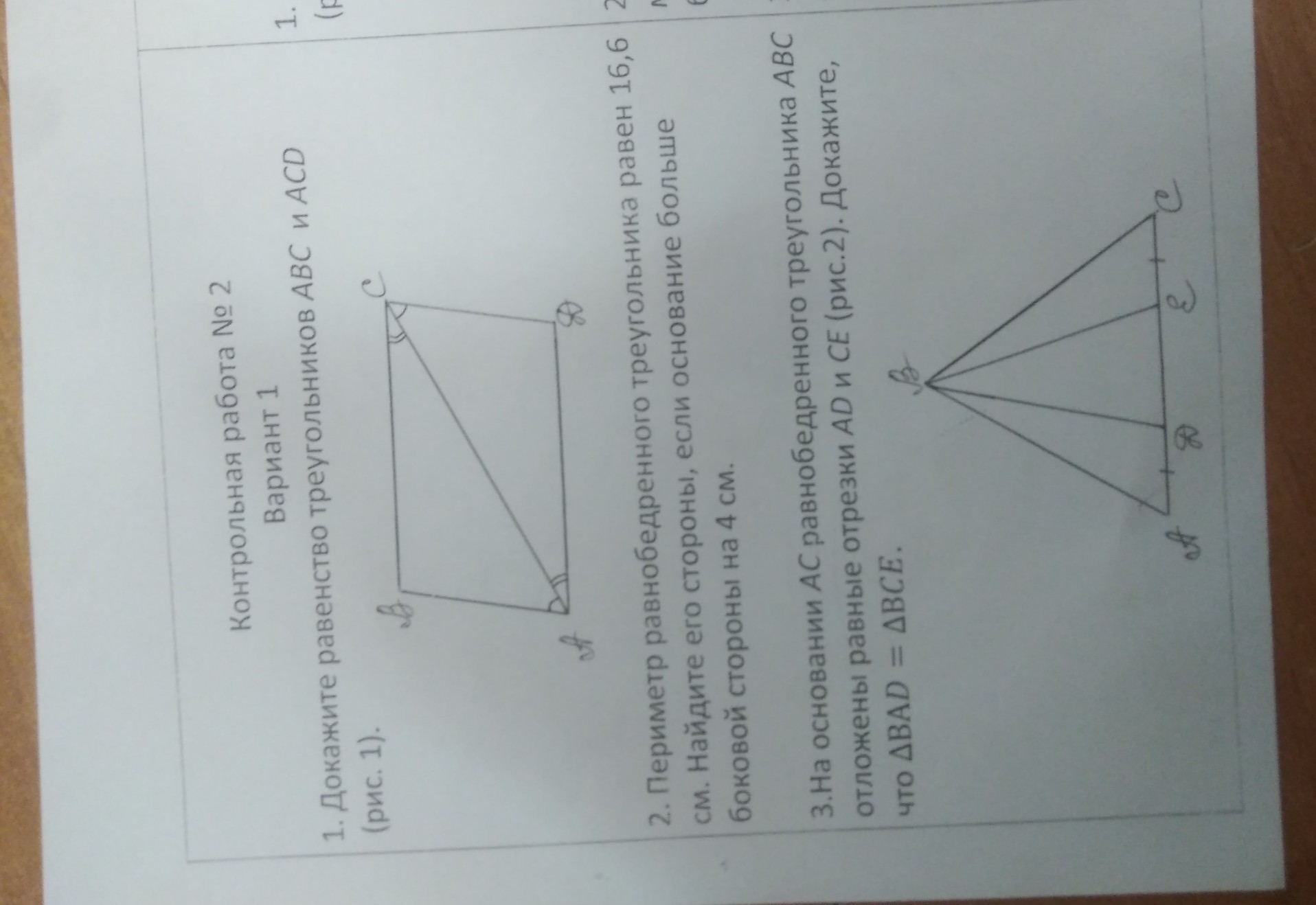
1. Дано: ΔABC; ΔACD; ∠BAC = ∠ACD; ∠ACB = ∠CAD.

Док-ть: ΔABC = ΔACD.

Док-во:

1) ∠BAC = ∠ACD (по условию).

2) ∠ACB = ∠CAD (по условию).

3) AC - общая сторона.

⇒ ΔABC = ΔACD (по 2-ому признаку равенства ΔΔ) ч.т.д.

2. Дано: ΔABC - равнобедренный; = 16,6 см; AC = AB + 4.

Найти: AB, BC, AC - ?

Решение:

Пусть AB = x, тогда, т.к. AB = BC, AC = AB + 4 и = AB + BC + AC,  x + x + (x + 4) = 16,6

x + x + x + 4 = 16,6

3x = 16,6 - 4

3x = 12,6

x =

x = 4,2

Ответ: 4,2.

3. Дано: ΔABC - равнобедренный; AD = CE.

Док-ть: ΔBAD = ΔBCE.

Док-во:

1) AD = CE (по условию).

2) AB = BC, т.к. ΔABC - равнобедренный по условию.

3) ∠A = ∠C, т.к. ΔABC - равнобедренный по условию.

⇒ ΔBAD = ΔBCE (по 1-ому признаку равенства ΔΔ) ч.т.д.

1. дано: угол bac = угол аcdугол acb = угол cadдоказать: треугольник abc =треуольник acd доказательство:рассмотрим треугольники abc и acd, в них:угол bac = угол аcd (по условию)угол acb = угол cad (по условию)ас - общая сторона значит, треугольники равны по стороне и углу между ними. 2. дано:равнобедренный треугольник abc P = 16.6ас - основание, на 4 см больше боковой сторонынайти: стороны треугольникарешение:Р = ab+bc+ac ab = bc = х (боковые стороны равнобедренного треугольника)ac = х + 4ab = bc = 4.2 ac = 4.2 + 4 = 8.23. дано: равнобедренный треугольник abc доказать: треугольник bad = треугольник bceдоказательство:рассмотрим треугольники bad и bce, в них:ad = ec ( по условию ), ab = bc ( боковые стороны равнобедренного треугольника ), угол bac = угол bca ( углы при основании равнобедренного треугольника )значит, треугольники bad и bce равны по 2 сторонам и углу между ними