-
В равнобедренном треугольнике с длиной основания 79 cм проведена биссектриса угла∡ABC. Используя второй признак равенства треугольников, докажи, что отрезок BD является медианой и определи длину отрезка AD.
Рассмотрим треугольники ΔABD и Δ
(треугольник записать в алфавитном порядке).
1. так как прилежащие к основанию углы данного равнобедренного треугольника равны, то ∡A=∡
;
2. так как проведена биссектриса, то ∡
=∡CBD;
3. стороны AB=CB у треугольников ΔABD и ΔCBD равны, так как данный ΔABC —
.
По второму признаку равенства треугольников ΔABD и ΔCBD равны.
Значит равны все соответсвующие элементы, в том числе стороны AD=CD. А это означает, что отрезок BD является медианой данного треугольника и делит сторону AC пополам.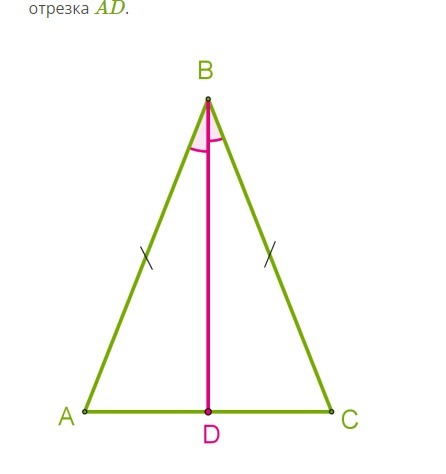
-
Предмет:
Геометрия -
Автор:
cold frontpytt - 6 лет назад
-
Ответы 1
-
1. угол а= углу с
2 ровняется углу abd
3 равнобедренный
-
Автор:
ruthiemaddox - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
усі цілі відємні числа , що більші за числа -4,2
-
Предмет:
Математика -
Автор:
buckeyestone - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Переставить элементы в обратном порядке c++
-
Предмет:
Информатика -
Автор:
rangel - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Прав ли был применительно к нашему времени Конфуций,считавший,что воспитанного человека легко узнать по его поведению???
-
Диалог на тему : Для чего нужна красная книга?
-
Предмет:
Русский язык -
Автор:
cassie - 6 лет назад
-
Ответов:
4 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
