-
Помогите с геометрии, даю 50 баллов.
Дали на каникулы.
8 класс. Тема: Решение прямоугольных треугольников
1) На рисунке (на фото) - прямоугольный треугольник ABC (∠C = 90 °). найдите:
1. cos A
2. sin B
3. tg A
4. cos B
2) Точка находится на расстоянии 4 см от прямой. С этой точки до прямой проведения наклонную, что образует с прямой угол 45 °. Найдите длину наклонной и длину проекции наклонной на прямую.
3) В прямоугольном треугольнике ABC (∠C = 90 °) AC = 8 см, cos∠A = 4/5. Найдите второй катет и гипотенузу треугольника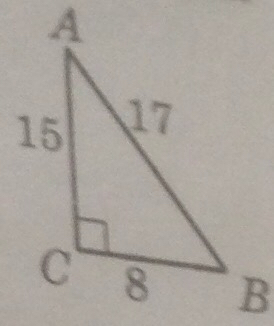
Ответы 3
-
СПАСИБО БОЛЬШОЕ!!!!
-
Автор:
best46 - 6 лет назад
-
0
-
-
Вот решение всех задач

-
Автор:
constantinoabtg - 6 лет назад
-
0
-
-
1)
2) Точка М , прямая а , МН⊥ а , МН=4 см , МК - наклонная, ∠МКН=45°.
Так как ∠МКН=45°, то и ∠КМН=90°-∠МКН=45° .
Тогда ΔМКН - равнобедренный и МН=КН=4 см, то есть проекция наклонной - это КН=4 см.
Наклонная МК=√(МН²+КН²)=√(4²+4²)=√2·16=4√2 (см).
Или МК=МН:sin∠МКН=4:(√2/2)=(4·2)/√2=4√2 (см) .
3) ΔАВС , ∠С=90° , АС=8 см , cos∠А=4/5 .

-
Автор:
herman - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Здравствуйте!
Задача по статистике.
Дано:
Оценки учеников: 90 80 70 60
Число учеников: 1 11 х 7
Средняя оценка: 72,5 по классу
Вопрос, сколько учеников получили оценку 70?-
Предмет:
Математика -
Автор:
jaylonvsrq - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
На десяти прозрачных карточках записаны числа от 0 до 9, далее на картинке вопрос. срочно. спасибо.
-
Предмет:
Математика -
Автор:
cheerio - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Найти минимальное количество битов с помощью которых можно представить каждое из перечисленных ниже беззнаковых двоичных целых чисел:a)65,б)256 в)32768,г)4095,д)65534,е)2134657
-
Предмет:
Информатика -
Автор:
gretamnjt - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Система земледелия, при которой определенный участок леса сначала вырубается, затем выжигается и вспахивается, называется
-
Предмет:
Биология -
Автор:
tayloresp4y - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
