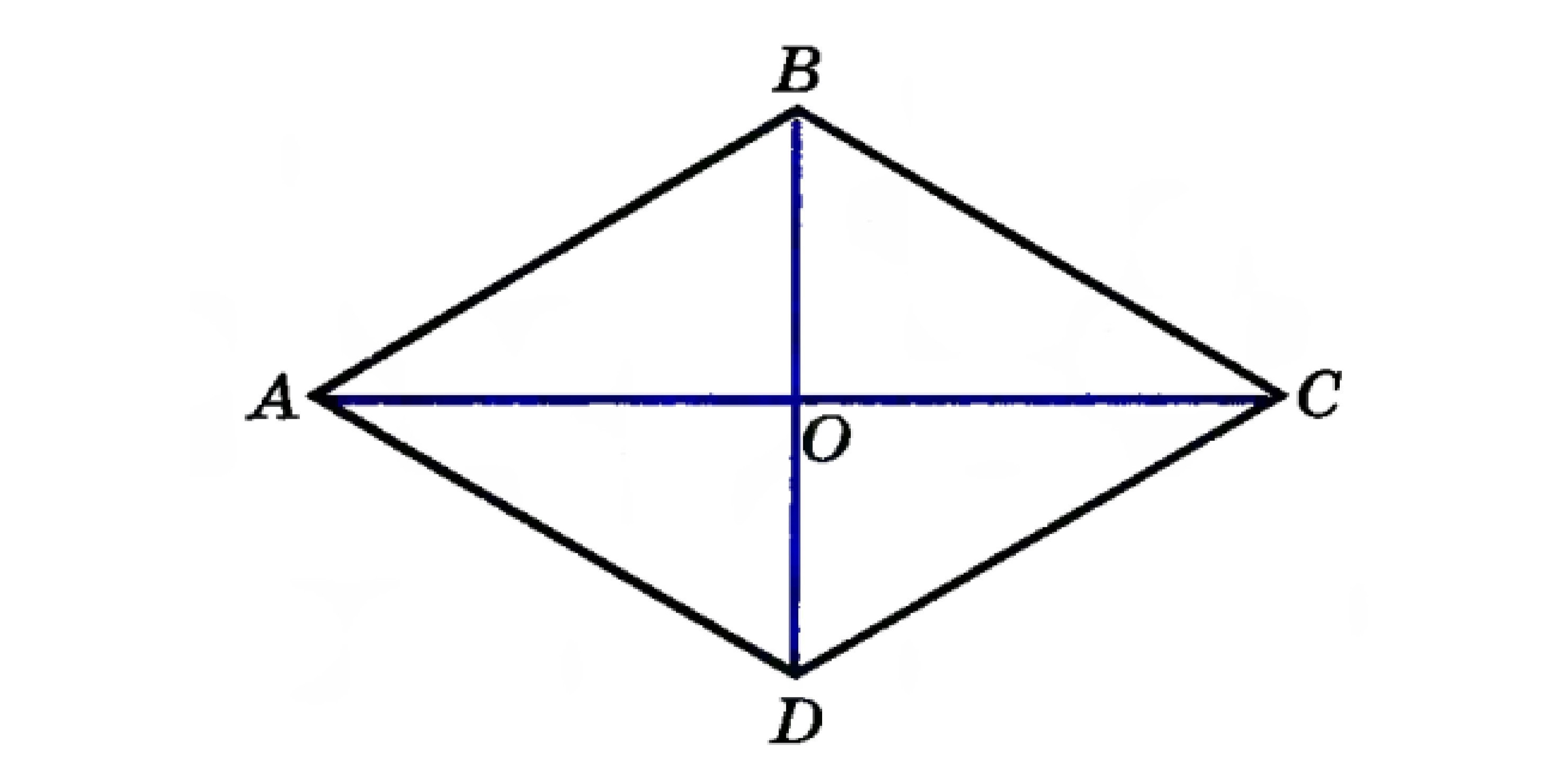
Найдите углы ромба ABCD, если его диагонали AC и BD равны 4 м и 8 м.Нужен полный аргументированный ответ

Рассмотрим любой из четырех равных прямоугольных треугольников внутри ромба например: треугольник AOB.Т.к. АС=4, BD=8, то АО=2, ВО=4Найдём углы OAB и OBA, с помощью тангенса угла (отношение противолежащего катета к прилежащему).tgOAB=4/2=2=> OAB=arctg2tgOBA=2/4=1/2 => OBA=arctg(1/2)Получаем: A=C=2*arctg2B=C=2*arctg(1/2)

АВСД - ромб  ⇒  АВ=ВС=СД=АД ,  АС=8 , ВД=4 .

Диагонали ромба перпендикулярны и в точке пересечения делятся пополам  ⇒  ∠АОВ=∠ВОС=∠АОД=∠СОД=90° ,  АО=СО=8:2=4 , ВО=ДО=4:2=2   ⇒  ΔАОВ=ΔАОД=ΔВОС=ΔДОС   (по двум катетам) ⇒  ∠ОАВ=∠ОАД=∠ВСО=∠ДСО ,  ∠ОВА=∠ОВС=∠ОДС=∠ОДА  ⇒  ∠ВАД=2·∠ОАВ , ∠АВС=2·∠АВО .

Рассмотрим ΔАОВ.  ΔАО=4 , ВО=2  ⇒  tg∠ОАВ=BO/AO=2/4=1/2  ⇒  ∠ОАВ=arctg(1/2) . Противоположные углы ромба равны, поэтому   ∠ВАД=∠АДС=2·arctg(1/2) .

tg∠АВО=АО/ВО=4/2=2  ⇒  ∠АВО=arctg2  и  ∠ABC=∠АДС=2·arctg2 .