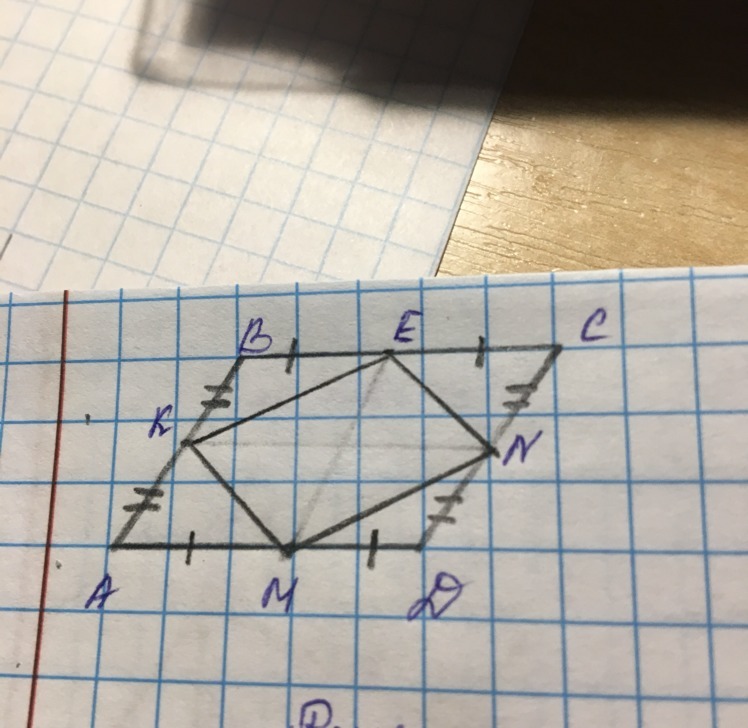
Помогите решить задачу. Геометрия. Дан параллелограмм АBCD. Площадь - ABCD=112 см квадратных. E,N,K,M - середины сторон. Найти: Площадь - ENMK

Подскажите пожалуйста, я в 8 классе, и мы ещё не изучали теорему Вариньона, можно ли другим способом решить задачу?

Средняя линия KN равна основаниям параллелограмма. Сумма высот треугольников KEN и KMN равна высоте параллелограмма. Следовательно сумма площадей этих треугольников равна половине площади параллеограмма.KN=BC=AD=a, H -высота параллелограмма, h1,h2 -высоты треугольников.S1+S2 =ah1/2+ah2/2 =(h1+h2)a/2 =aH/2 =Sпар

S1+S2 =ah1/2+ah2/2 =(h1+h2)a/2 =aH/2 =Sпар/2

Середины сторон произвольного четырёхугольника являются вершинами параллелограмма (теорема Вариньона). Площадь параллелограмма Вариньона равна половине площади исходного четырёхугольника.

S(ENMK)= S(ABCD)/2 =112/2 =56   (см^2)

Средняя линия треугольника параллельна основанию и равна его половине, следовательно отсекает подобный треугольник с коэфф. подобия 1/2. Площади подобных фигур относятся как квадрат коэфф. подобия. Отсекаемый треугольник равен 1/4 площади исходного.

KE - средняя линия в ABC, S(KBE)=S(ABC)/4

MN - средняя линия в ADC, S(MDN)=S(ADC)/4

S(KBE)+S(MDN) =S(ABC)/4 +S(ADC)/4 =S(ABCD)/4

Аналогично S(KAM)+S(ECN) =S(ABCD)/4

S(KBE)+S(MDN)+S(KAM)+S(ECN) =S(ABCD)/2

Отсекаемые средними линиями треугольники в сумме равны половине площади исходного четырехугольника. Следовательно, параллелограмм Вариньона также равен половине площади исходного четырехугольника.