-
PN=NT,PK-биссектриса угла MPT,угол NPT=70*,угол PKM=55*
Докажите, что прямые PTи MK параллельны.Найдите угол PKT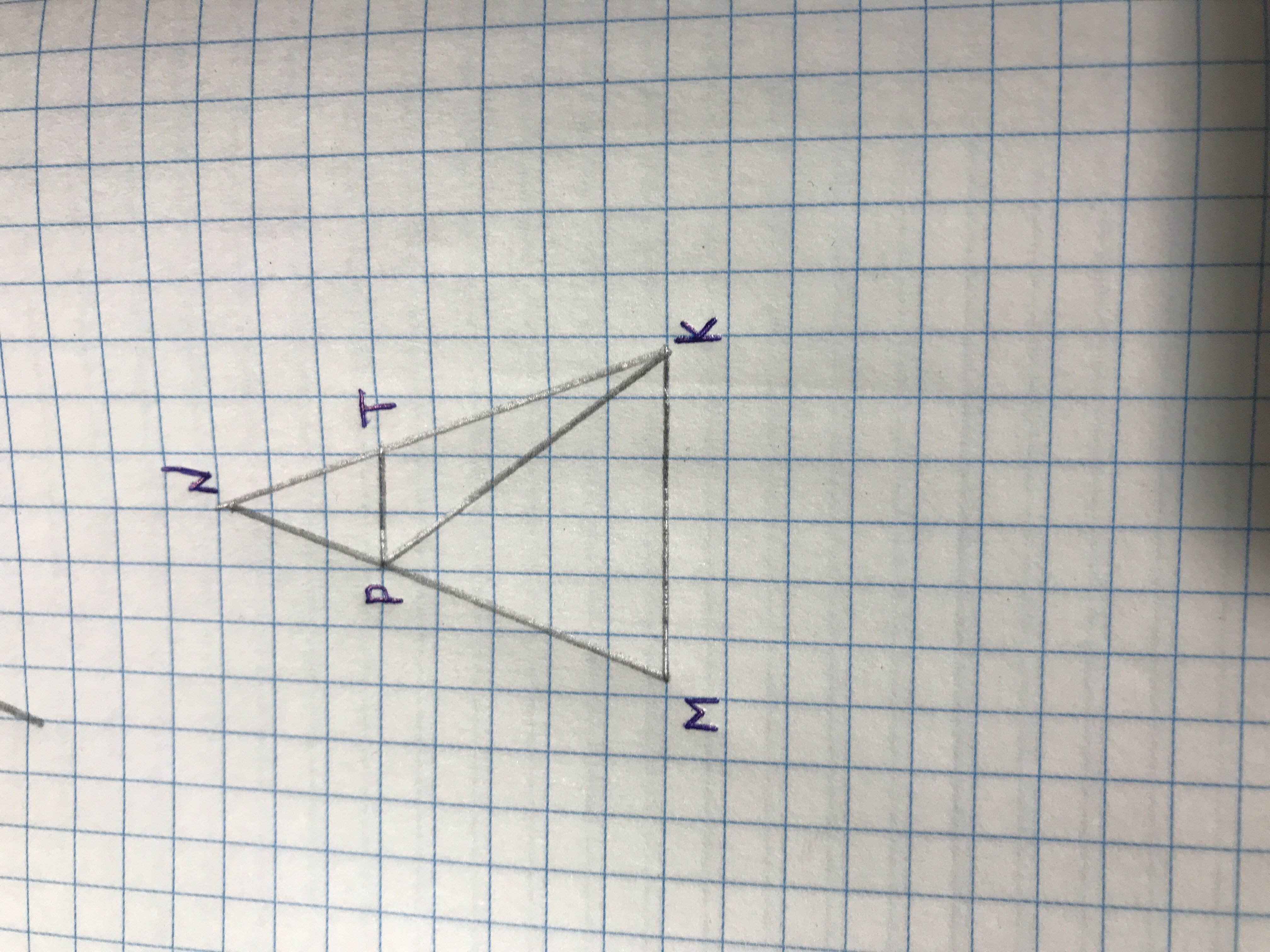
Ответы 1
-
Смежные углы составляют развернутый угол, 180.
∠MPT=180-∠NPT =180-70=110 (∠MPT, ∠NPT - смежные углы)
Биссектриса делит угол пополам.
∠TPK=∠MPT/2 =110/2=55 (PK - биссектриса ∠MPT)
Если накрест лежащие углы равны, то прямые параллельны.
∠TPK=∠PKM => PT||MK (∠TPK, ∠PKM - накрест лежащие углы)
Углы при основании равнобедренного треугольника равны.
△PNT - равнобедренный (PN=NT) => ∠NTP=∠NPT =70 (углы при основании △PNT)
Внешний угол треугольника равен сумме внутренних, не смежных с ним.
∠PKT=∠NTP-∠TPK =70-55=15 (∠NTP - внешний угол △PKT)
-
Автор:
frankie63 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Поставить скобки чтобы получилось 17
7* 8 + 4:4+2=17-
Предмет:
Математика -
Автор:
gaugew1mf - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
3-4 оценки личности Ивана Грозного,историками и писателями.
-
Предмет:
Математика -
Автор:
pigletkyqu - 6 лет назад
-
Ответов:
5 -
Смотреть
-
-
Напишите пословицы ,употребляя слова в скобках в настоящем времени.
1)У ленивого и крыша (течь),и печ не(печь).2) Минута час (беречь).3)Пуля (стеречь) да каска (беречь).4)Этот парикмахер очень хорошо (стричь).5)Мастер (ткать) полотно.6)Новое место всегда (влечь) туристов .7)Жаркое солнце сильно (печь).
-
Предмет:
Русский язык -
Автор:
patchhowe - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
Как будет по украинскому пуфик?
-
Предмет:
Українська мова -
Автор:
cassandrawaxw - 6 лет назад
-
Ответов:
4 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
