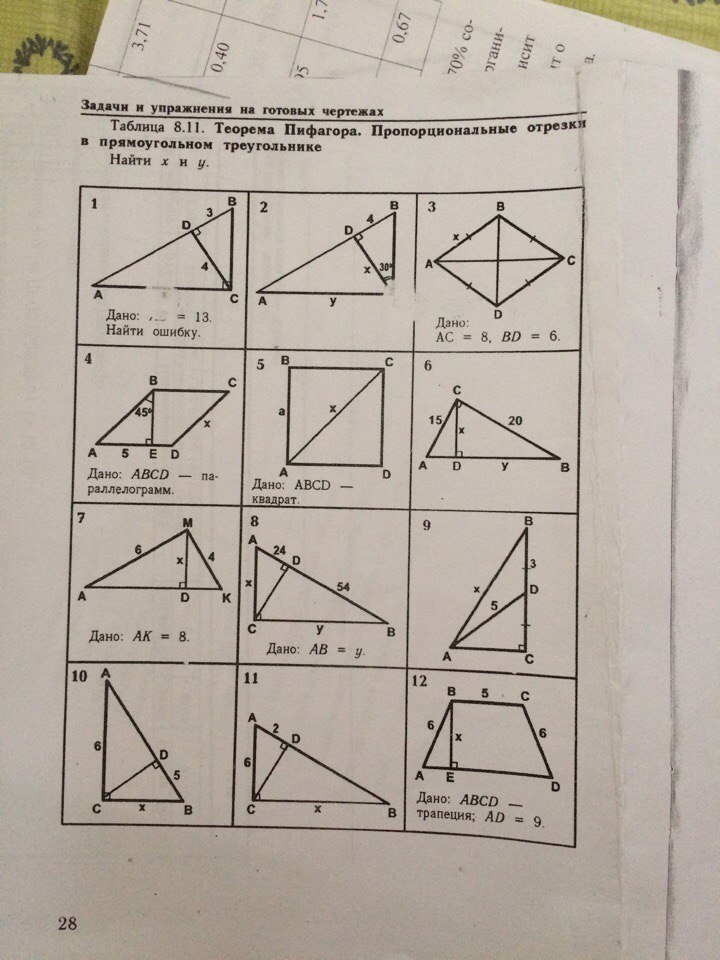
Таблица 8.11 Теорема Пифагора. Пропорциональные отрезки в прямоугольном треугольнике (решите хотя бы 1-9 пожалуйста)

 c2 = a2 + b2 - теорема Пифагора, просто подставь значения катетов в "a" и "b", и готово.

Теорема Пифагора:

c² = a² + b²

Свойства пропорциональных отрезков в прямоугольном треугольнике:

(см. рисунок)

1. AD = AB - DB = 13 - 3 = 10

По свойству пропорциональных отрезков должно выполняться равенство:

CD² = AD · DB

16 = 10 · 3

16 = 30 - неверно

Значит, ошибка в данных длинах отрезков.

Если CD = 4 и DB = 3, то

AD = CD² / DB = 16/3

По теореме Пифагора:

Но тогда АВ = AD + DB = 16/3 + 3 = 25/3, а не 13, как дано по условию.

2. ΔDBC: 

BC = 2BD = 2 · 4 = 8 по свойству катета, лежащего напротив угла в 30°,

По теореме Пифагора:

x = √(BC² - BD²) = √(64 - 16) = √48 = 4√3

BC² = AB · BD, ⇒

AB = BC² / BD = 64 / 4 = 16

Из ΔАВС по теореме Пифагора

y = √(AB² - BC²) = √(256 - 64) = √192 = 8√3

3. ABCD - ромб, значит его диагонали перпендикулярны и точкой пересечения делятся пополам. Обозначим точку пересечения диагоналей О.

АО = АС/2 = 4

ВО = BD/2 = 3

Из ΔАОВ по теореме Пифагора:

x = √(AO² + BO²) = √(16 + 9) = √25 = 5

4. ΔABE: ∠AEB = 90°, ∠ABE = 45°, ⇒ ∠BAE = 90° - 45° = 45°,

значит треугольник равнобедренный, BE = AE = 5,

по теореме Пифагора

AB = √(AE² + BE²) = √(25 + 25) = √50 = 5√2

Противолежащие стороны параллелограмма равны, ⇒

x = AB = 5√2

5. Все стороны квадрата равны. ВС = АВ = а.

Из треугольника АВС по теореме Пифагора:

x = √(AB² + BC²) = √(a² + a²) = √(2a²) = a√2

6. По теореме Пифагора

AB = √(AC² + BC²) = √(225 + 400) = √625 = 25

По свойству пропорциональных отрезков:

CB² = AB · y

y = CB² / AB = 400 / 25 = 16

AD = AB - y = 25 - 16 = 9

x² = AD · y = 9 · 16

x = √(9 · 16) = 3 · 4 = 12

7. AK² = 64

AM² + MK² = 36 + 16 = 52

AK² ≠ AM² + MK², значит по теореме, обратной теореме Пифагора, треугольник не прямоугольный.

Пусть DK = a, тогда AD = 8 - a.

Из ΔAMD по теореме Пифагора:

x² = AM² - AD²

x² = 36 - (8 - a)² = 36 - 64 + 16a - a² = - 28 + 16a - a² (1)

Из ΔMDK по теореме Пифагора:

x² = MK² - DK²

x² = 16 - a² (2)

Приравняем (1) и (2):

- 28 + 16a - a² = 16 - a²

16a = 44

a = 11/4

Подставим в (2):

8. CD = √(AD · DB) = √(24 · 54) = √(4 · 6 · 6 · 9) = 2 · 6 · 3 = 36

ΔADC: по теореме Пифагора

       x = √(AD² + CD²) = √(576 + 1296) = √1872 = 12√13

ΔBCD: по теореме Пифагора 

      y = √(CD² + BD²) = √(1296 + 2916) = √4212 = 18√13

9. AD - медиана, значит DC = BD = 3,  BC = 2BD = 6.

ΔADC: по теореме Пифагора

      AC = √(AD² - DC²) = √(25 - 9) = √16 = 4

ΔABC: по теореме Пифагора

      x = √(BC² + AC²) = √(36 + 16) = √(52) = 2√13

10. По свойству пропорциональных отрезков

x² = AB · BD = 5AB  (1)

Из ΔАВС по теореме Пифагора

x² = AB² - AC²

Подставим (1):

5AB = AB² - 36

AB² - 5AB - 36 = 0

D = 25 + 144 = 169

AB = (5 + 13)/2 = 9

AB = (5 - 13)/2 = - 4 - не подходит по смыслу задачи.

x² = 5 · 9 = 45

x = 3√5

11. AC² = AB · AD, ⇒ AB = AC² / AD = 36 / 2 = 18

ΔABC: по теореме Пифагора

       x = √(AB² - AC²) = √(324 - 36) = √288 = 12√2

12. Проведем высоту СК. ЕВСК - прямоугольник (все углы прямые), значит ЕК = ВС = 5.

ΔABE = ΔDСK по катету и гипотенузе (ВЕ = СК как высоты, АВ = CD по условию), ⇒

АЕ = KD = (AD - EK) / 2 = (9 - 5)/2 = 2

ΔABE: по теореме Пифагора

      x = √(AB² - AE²) = √(36 - 4) = √32 = 4√2