Задать вопрос Регистрация
Помочь другим

  • В треугольнике ABC: AB=BC=5, AC=6.
    Найдите sin(B), cos(B), tan(B)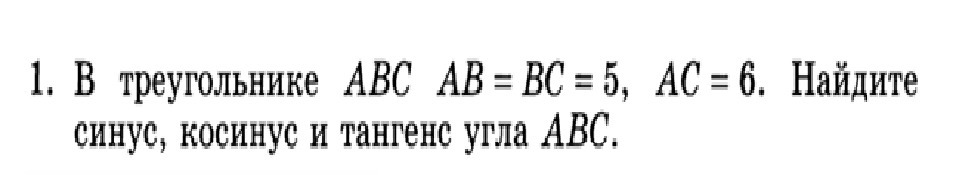

    question img

Ответы 6

  • да, но мне кажется, решение должно быть легче

    • Автор:

      emmyaic5
    • 5 лет назад
    • 0
  • другие задачи из этой серии куда легче, => сюда их я даже и не выкладываю
  • я тут формулу нашел типа sin(a+b) = sin(a)*cos(b) + cos(a)*sin(b)

    • Автор:

      giovanny
    • 5 лет назад
    • 0
  • вышло также 0.96

    • Автор:

      autumn84
    • 5 лет назад
    • 0
  • откуда нашли sin(b) и cos(b)

    • Автор:

      girldltd
    • 5 лет назад
    • 0

  • По формуле Герона:

    S=\sqrt{p(p-a)(p-b)(p-c)}, где p - полупериметр

    p=\frac{5+5+6}{2}=\frac{16}{2}=8\\S=\sqrt{8*(8-5)(8-5)(8-6)}=\sqrt{8*3*3*2}=\sqrt{2^{3}*3^{2}*2}=\\=\sqrt{2^{4}*3^{2} }=4*3=12\\

    Также, площадь треугольника равна:

    2S=AB*BC*sinB\\sin B=\frac{S}{AB*BC}=\frac{12}{5*5}=0.96

    Согласно основному тригонометрическому тождеству:

    sin^{2}B+cos^{2}B=1\\cos B=\sqrt{1-sin^{2}B }=\sqrt{1-(0.96)^{2}}=\sqrt{1-0.9216} = 0,28

    По определению тангенса:

    tgB=\frac{sinB}{cosB} = \frac{0.48}{0,28} = 1,7142857142857142857142857142857

    Ответ:  sin B = 0.96, cos B = 0.28, tg B = 1.71

    • Автор:

      knight
    • 5 лет назад
    • 0

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years