Ответы 1
-
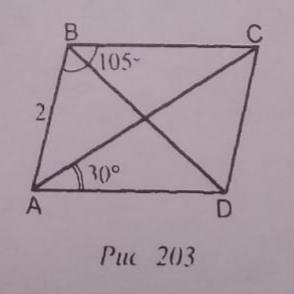
Дано: АВСD - параллелограмм.
<ABC = 105°, <CAD = 30°, AB = 2 ед.
Тогда <BAD = 180-105 = 75° (сумма углов, прилежащих к одной стороне параллелограмма, равна 180°), а <BAC=75-30 = 45°.
Опустим перпендикуляр ВН на диагональ АС. Тогда в прямоугольном треугольнике АВН острые углы равны по 45° и катеты
ВН = АН = √2 ед.
В треугольнике ВНС угол
<НВС = 105-45=60°, a <BCH = 30° (по сумме острых углов прямоугольного треугольника =90°).
Против угла 30° лежит катет, равный половине гипотенузы. =>
ВС = 2√2 ед.
-
Автор:
page - 5 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Даю 30 баллов
Помогите пожалуйста!!!
СРОЧНО!!!!!!
-
Предмет:
Русский язык -
Автор:
young - 5 лет назад
-
Ответов:
1 -
Смотреть
-
- почему бабочки летают беззвучно
-
1) В программе «:=» обозначает оператор присваивания, знаки «+», «–», «*» и «/» – соответственно операции сложения, вычитания, умножения и деления. Правила выполнения операций и порядок действий соответствует правилам арифметики.
Определите значение переменной m после выполнения данного алгоритма:
k := 3
m := 30
k := m-k*3
m := k*10-m
В ответе укажите одно целое число — значение переменной m.
2) В программе «:=» обозначает оператор присваивания, знаки «+», «-», «*» и «/» — соответственно операции сложения, вычитания, умножения и деления. Правила выполнения операций и порядок действий соответствуют правилам арифметики. Определите значение переменной a после выполнения алгоритма:
а := 6
b := 4
b := a/2*b
a := 2*а + 3*b
В ответе укажите одно целое число — значение переменной a.
3)
В программе «:=» обозначает оператор присваивания, знаки «+», «-», «*» и «/» — соответственно операции сложения, вычитания, умножения и деления. Правила выполнения операций и порядок действий соответствуют правилам арифметики. Определите значение переменной b после выполнения алгоритма:
а := 1
b := 27
a := b/a*2
b := a*2 - 8
В ответе укажите одно целое число — значение переменной b.
4)
В алгоритме, записанном ниже, используются переменные a и b.
Символ «:=» обозначает оператор присваивания, знаки «+», «-», «*» и «/» − операции сложения, вычитания, умножения и деления. Правила выполнения операций и порядок действий соответствует правилам арифметики.
Определите значение переменной а после выполнения данного алгоритма:
a := 5
b := 6
b := 5 + a * b
a := b – 6 * a
В ответе укажите одно целое число − значение переменной а.
5) В программе «:=» обозначает оператор присваивания, знаки «+», «−», «*» и «/» − соответственно операции сложения, вычитания, умножения и деления. Правила выполнения операций и порядок действий соответствует правилам арифметики.
Определите значение переменной а после исполнения данного алгоритма:
a := 36
b := a / 12
b := b + a / 4
a :=a / b * 3
В ответе укажите одно число − значение переменной а.
6) В программе «:=» обозначает оператор присваивания, знаки «+», «-», «*» и «/» — соответственно операции сложения, вычитания, умножения и деления. Правила выполнения операций и порядок действий соответствуют правилам арифметики. Определите значение переменной a после выполнения алгоритма:
а := 6
b := 2
b := a/2*b
a := 2*а + 3*b
В ответе укажите одно целое число — значение переменной a.
7) В программе «:=» обозначает оператор присваивания, знаки «+», «-», «*» и «/» — соответственно операции сложения, вычитания, умножения и деления. Правила выполнения операций и порядок действий соответствуют правилам арифметики. Определите значение переменной b после выполнения алгоритма:
а := 7
b := 5
а := b*4 - a*2
b := а*4 - 4
В ответе укажите одно целое число — значение переменной b.
8) В программе «:=» обозначает оператор присваивания, знаки «+», «-», «*» и «/» — соответственно операции сложения, вычитания, умножения и деления. Правила выполнения операций и порядок действий соответствуют правилам арифметики. Определите значение переменной a после выполнения алгоритма:
b := 6
a := 30
b := b*4–21
a := 100–a–b
В ответе укажите одно целое число — значение переменной a.
9) В программе «:=» обозначает оператор присваивания, знаки «+», «–», «*» и «/» – соответственно операции сложения, вычитания, умножения и деления. Правила выполнения операций и порядок действий соответствует правилам арифметики.
Определите значение переменной a после выполнения данного алгоритма:
a := 6
b := 2
b := a/2*b
a := 2*a+3*b
В ответе укажите одно целое число — значение переменной a.
10) В программе «:=» обозначает оператор присваивания, знаки «+», «–», «*» и «/» – соответственно операции сложения, вычитания, умножения и деления. Правила выполнения операций и порядок действий соответствует правилам арифметики.
Определите значение переменной a после выполнения данного алгоритма:
a := 7
с := 3
с := 3 + a * с
a := с / 3 * a
В ответе укажите одно целое число — значение переменной a.-
Предмет:
Информатика -
Автор:
page - 5 лет назад
-
Ответов:
6 -
Смотреть
-
-
Помогите плиз, листочик прекрепил
2-3 задания
1 вариант только-
Предмет:
Математика -
Автор:
tannertswh - 5 лет назад
-
Ответов:
2 -
Смотреть
-
Топ пользователей
-
Fedoseewa27
35894 -
Askold
2792 -
Pikachu
2224 -
hobbesbowers
2116 -
kaylynnbarron676
1818 -
女fei
1240 -
yulia-kaplina
1156 -
Poinntt
946 -
Bars
930 -
Queenmagic18
754
How much to ban the user?
1 hour
1 day
100 years