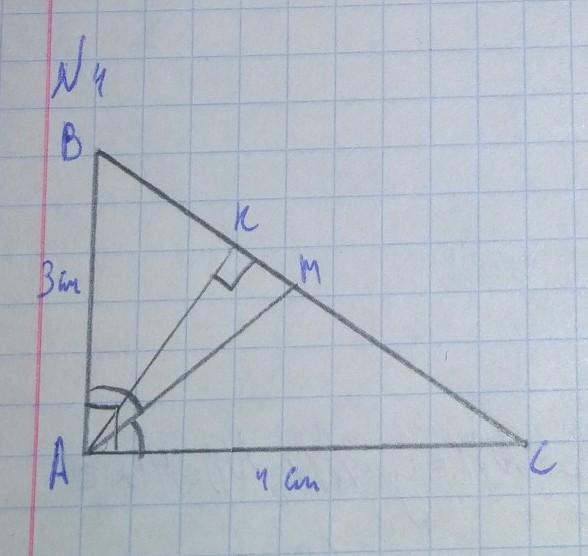
В треугольнике АВС с прямым углом А проведены высота AК и биссектриса АМ. Найдите КМ, если АВ=3

В треугольнике АВС с прямым углом А проведены высота AК и биссектриса АМ. Найдите КМ, если АВ=3 см АС =4 см. (см.чертеж)
- Предмет:
  Геометрия
- Автор:
  gloriabowman131
- 5 лет назад

Ответы 5

Только AK можно проще найти, по свойству пропорциональных отрезков
- Автор:
  manueleuc8
- 5 лет назад
- 0
И по сути AK тут и не нужно
- Автор:
  skipperlill
- 5 лет назад
- 0
Дело Ваше:) Решений то много у задачи
- Автор:
  buttonspierce
- 5 лет назад
- 0
Я просто говорю тем, кто будет просматривать. Мне бы на ваше решение сказали:"не рационально" и поставили бы 2
- Автор:
  louiebwdj
- 5 лет назад
- 0
1. По теореме Пифагора из ΔABC найдём BC:
$BC=\sqrt{AC^2+AB^2}=\sqrt{16+9}=\sqrt{25}=5cm$
2. SΔABC можно найти разными способами:
$S\Delta ABC= \frac{1}{2}AB \cdot AC = \frac{1}{2}\cdot 3 \cdot 4 = 6 cm^2$
$S\Delta ABC= \frac{1}{2}BC \cdot AK=\frac{5}{2} AK$
Откуда можно найти AK:
$\frac{5}{2}AK=6\\ 5AK=12\\ AK=\frac{12}{5}cm$
3. По теореме Пифагора из ΔABK найдём BK:
$BK=\sqrt{AB^2-AK^2}=\sqrt{9-\frac{144}{25}}=\sqrt{\frac{225-144}{25}}=\sqrt{\frac{81}{25}}=\frac{9}{5}cm$
4. $KC=BC-BK=5-\frac{9}{5}=\frac{25-9}{5}=\frac{16}{5}cm$
5. Пусть x=KB, тогда $BM=\frac{9}{5}+x,MC=\frac{16}{5}-x$
Используя свойство биссектрисы треугольника, составим уравнение:
$\frac{AC}{MC}=\frac{AB}{BM}\\ \\ \frac{4}{\frac{16}{5}-x}=\frac{3}{\frac{9}{5}+x}\\ \\ \frac{4}{\frac{16-5x}{5}}=\frac{3}{\frac{9+5x}{5}}\\ \\ \frac{4\cdot 5}{16-5x}=\frac{3\cdot 5}{9+5x}\\ \\ \frac{4}{16-5x}=\frac{3}{9+5x}\\ \\ 4(9+5x)=3(16-5x)\\ 36+20x=48-15x\\ 35x=12\\ \\ KM=x=\frac{12}{35}cm$
$OTBET: \frac{12}{35}cm$
- Автор:
  taliyahhenson
- 5 лет назад
- 0
Добавить свой ответ

Еще вопросы

В треугольнике АВС с прямым углом А проведены высота AК и биссектриса АМ. Найдите КМ, если АВ=3 см АС =4 см. (см.чертеж)​

Ответы 5

Топ пользователей

В треугольнике АВС с прямым углом А проведены высота AК и биссектриса АМ. Найдите КМ, если АВ=3 см АС =4 см. (см.чертеж)