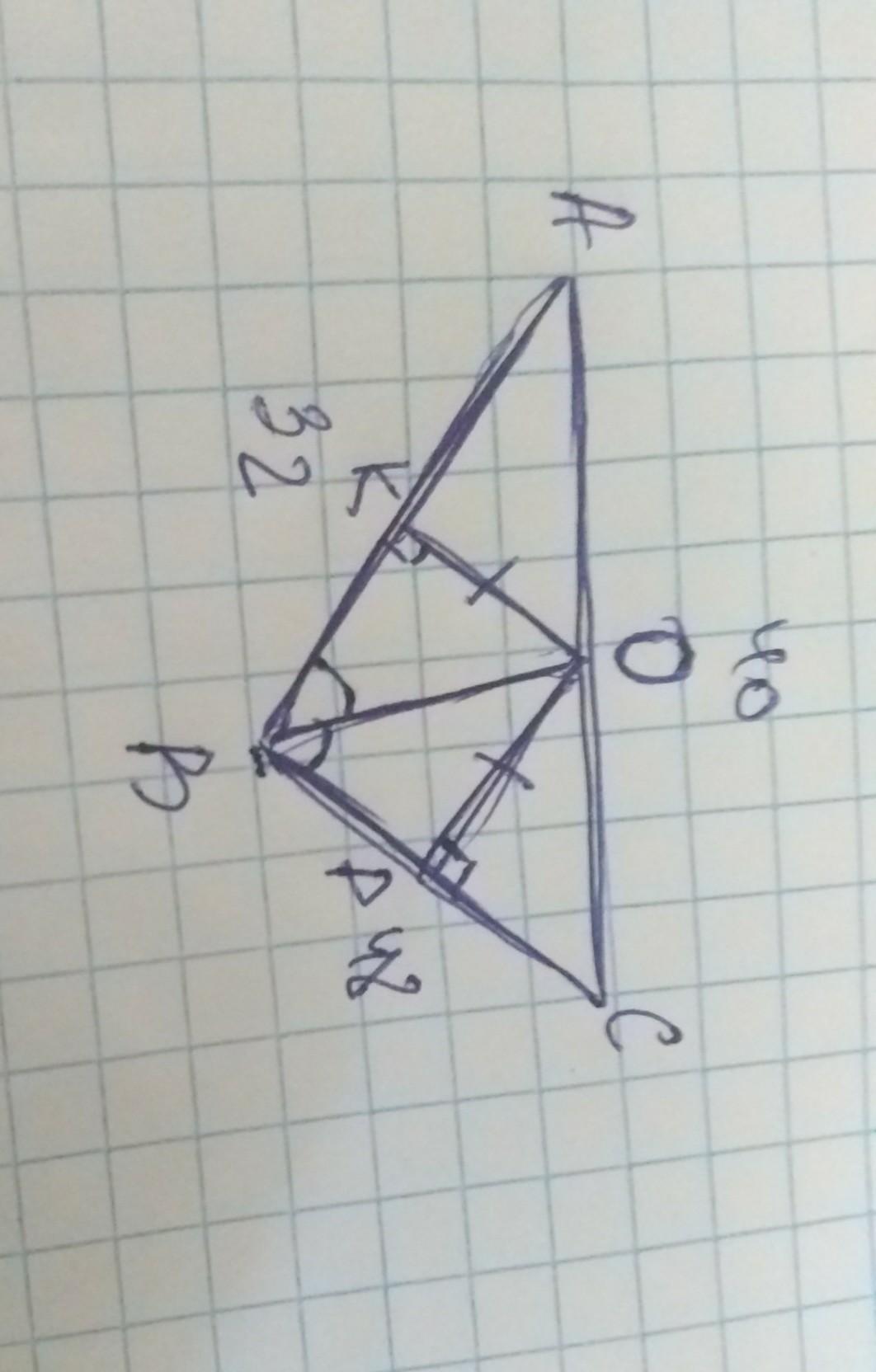
как найти OK? Даны все стороны треугольника , ОВ - бисектриса, ОК=ОР , ОК и ОР перпендикулярны АВ ВС​

В треугольнике АВС ОВ - биссектриса угла В, так как точка О равноудалена от сторон АВ и ВС. Или в  треугольнике АВС ОК = ОР, так как ОВ - биссектриса. Нам дано и то и другое.

Треугольник АВС делится этой биссектрисой на два треугольника. Причем Sabc = Sabo + Scbo.

По Герону Sabc = √(p*(p-a)(p-b)(p-c)), где р - полупериметр треугольника АВС, равный (32+48+40):2 = 60.

Sabc = √(60*20*28*12) = 240√7.

Sabo = (1/2)*h*AB =16*h.

Scbo = (1/2)*h*BC = 24*h.

240√7 = 16h +24h =40h  =>  h = 6√7.

h = OK = OP.

Ответ: ОК=ОР = 6√7 ед.

Или так:

Площади треугольников с одинаковой высотой относятся как стороны, к которым проведена эта высота. то есть Sabo/Scbo = 32/48 = 2/3. Sabc = 240√7 (найдено выше) => Sabo = 96√7  => h =2S/AB = 192√7/32 = 6√7.