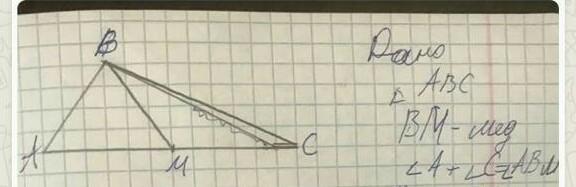
В треугольнике ABC. провели медиану BM. Оказалось, что сумма углов A и C равна углу ABM. Найдите отношение медианы BM

к стороне BC.(задача на продолжение медианы в свою длину)

​

    Примем  в  ∆ АВС ∠ВАС=а, ∠АСВ=с. Продолжим медиану на её длину до т.Д. Соединив вершины А и С с Д, получим параллелограмм АВСД (  из признака параллелограмма – диагонали точкой пересечения М делятся пополам). ∠САД=с (накрестлежащие при пересечении параллельных ВС и АД секущей АС).  Аналогично ∠АСД=а (накрестлежащий углу ВАС.

  По условию ∠АВМ=а+с. В ∆ АДВ углы при основании АВ равны а+с ⇒ АД=ВД. На том же основании  в ∆ ВСД углы при СД равны а+с, и ВС=ВД.  По построению ВМ=МД, ⇒ВМ =ВС:2, т.е. отношение медианы ВМ:ВС=1:2