-
1.Прямая АВ касается окружности с центром О радиуса r в точке В. Найдите АВ, если угол АОВ=60°,r=6 cm.
2.На рисунке : АВ и АС- касательные ВО=6см, АО=12 см. Найдите угол между касательными.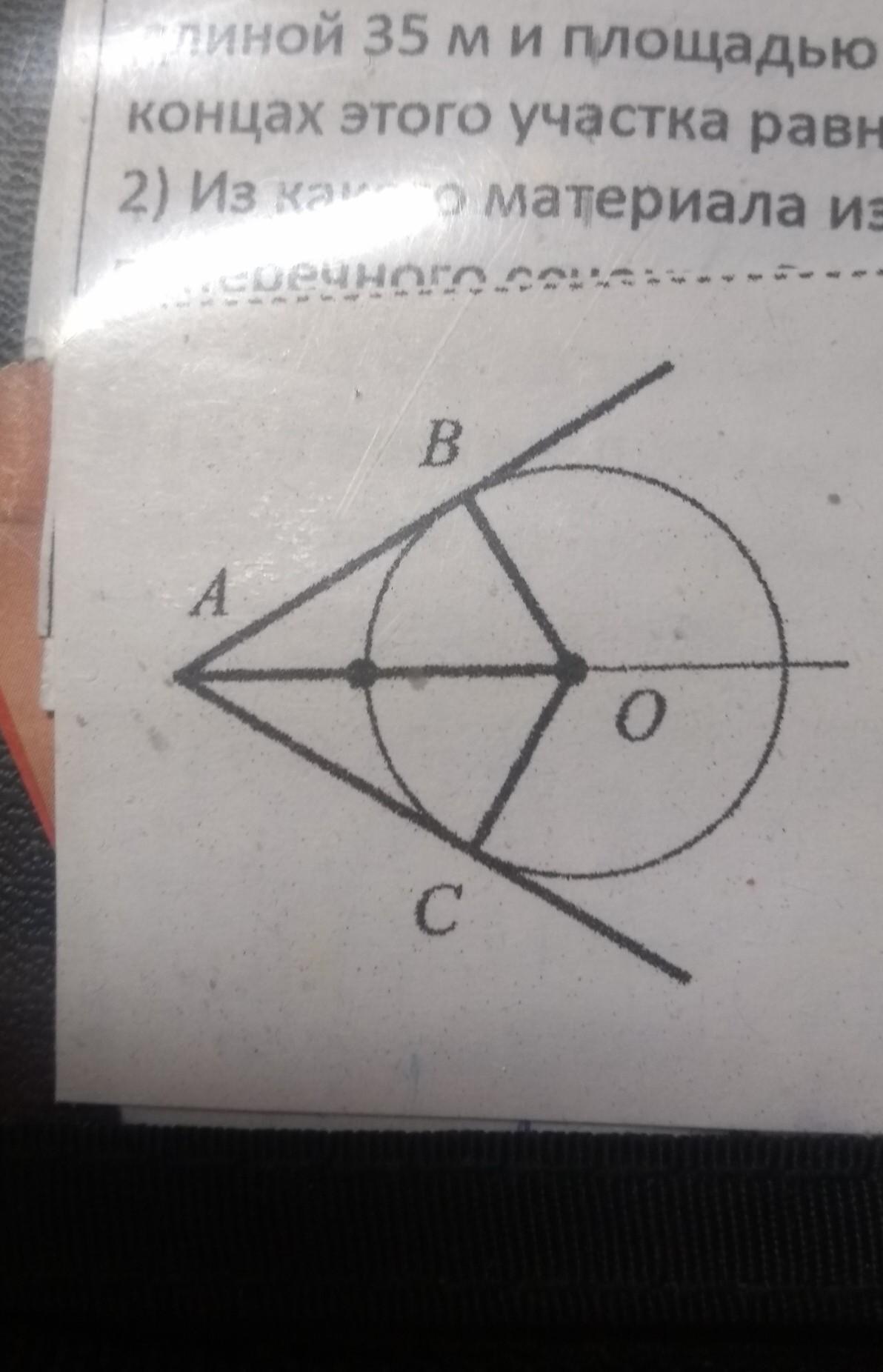
-
Предмет:
Геометрия -
Автор:
virginiaayala - 6 лет назад
-
Ответы 1
-
1)
AB⊥BO
AOB - прямоугольный треугольник
∠OAB = 180-90-60=30
Катет, противолежащий углу 30°, равен половине гипотенузы:
OB = AB/2
AB = 12
По теореме Пифагора, OB²+BA²=OA²
BA²=OA²-OB²
2)
BO=CO=6см
AB⊥ BO, AC⊥CO
ΔABO=ΔACO ⇒ ∠BAO = ∠CAO
BO - катет прямоугольного треугольника ABO. Катет, противолежащий углу 30°, равен половине гипотенузы.
Т.к. BO=AB/2, то ∠BAO = 30°.
∠BAO = ∠BAO+∠CAO = 30+30 = 60°
-
Автор:
kae - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Помогите, пожалуйста.
Add a question-tag to these sentences:
She likes quiet places, ______________________?
Tom didn’t play the piano, _______________________?
They didn’t hurt the child, _______________________?
There were two car accidents yesterday, _______________________?
Tourists used to come here, ________________________?
You haven’t got a computer, ________________________?
You don’t have to follow him, ________________________?
He has to fill a form, ________________________?
He didn’t have to choose one, _______________________?
He has your ticket, _______________________?
Everything is all right, _______________________?
He has got to leave, ______________________?
Smoking ruins our health, ________________________?
Most people cannot go to Africa, ________________________?
Finding a job isn’t easy, _______________________?-
Предмет:
Английский язык -
Автор:
coltonomjj - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Помоги пожалуйста, заранее огромное спасибо (хотя бы 1)
-
Предмет:
Математика -
Автор:
oliverchavez - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Від яких слів утворилися лексеми творчість, мужність?
-
Предмет:
Українська мова -
Автор:
javierjensen - 6 лет назад
-
Ответов:
1 -
Смотреть
-
- Таблица:северной америке, название климатического пояса, название природной зоны, климат, животный и растительный мир
How much to ban the user?
1 hour
1 day
100 years
