помогите пожалуйста решить прошу вас сделать это срочно!!!! ☺️☺️​

Рассмотрим треугольник RPS. По правилам прямоугольного треугольника мы видим, что катет в 2 раза меньше гипотенузы, а значит угол, лежащий против этой стороны равен 30°(<PRS)

Т.к. <PRS=<SRQ, то мы можем найти <RQP. <RQP=180-30-30-90=30°.Отсюда находим смежный с ним угол <RQT.

<RQT = 180-30=150°

Если <SRQ=<RQS,значит треугольник RSQ равнобедренный, и значит RS=SQ=15,6

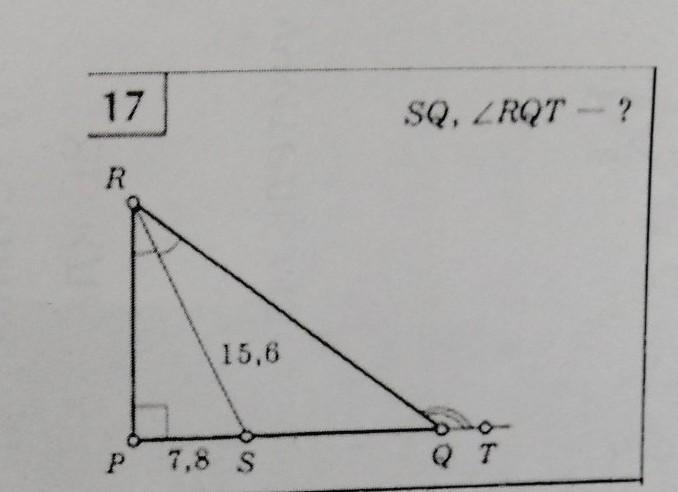
17. Дано: ΔPRT - прямоугольный с прямым углом P, RS - биссектриса, равная 15,6, PS = 7,8, ∠RQT - внешний.

Найти: SQ, ∠RQT - ?

Решение:

Рассмотрим ΔPRS - прямоугольный: RS = 15,6 - гипотенуза, PS = 7,8 - катет

∠R = 30° (катет, лежащий напротив угла в 30°, равен половине гипотенузы)

∠S = 90 - ∠R = 90 - 30 = 60° (сумма острых углов прямоугольного треугольника равна 90°)

∠PRS = ∠SRQ = 30° (RS - биссектриса)

∠RSQ = 180 - ∠PSR = 180 - 60 = 120° (смежные)

Рассмотрим ΔRSQ

∠R = 30°, ∠S = 120°, ∠Q - ?

∠Q = 180 - ∠R - ∠S = 180 - 30 - 120 = 30°

∠R = ∠Q = 30° ==> ΔRSQ - равнобедренный ==> RS = SQ = 15,6

∠RQT = 180 - ∠PQR = 180 - 30 = 150° (смежные)

Ответ: SQ = 15,6, ∠RQT = 150°