Задать вопрос Регистрация
Помочь другим

  • Срочно

    40 баллов!!!!

    Именно решение, не письменные объяснения, а формулы и решение.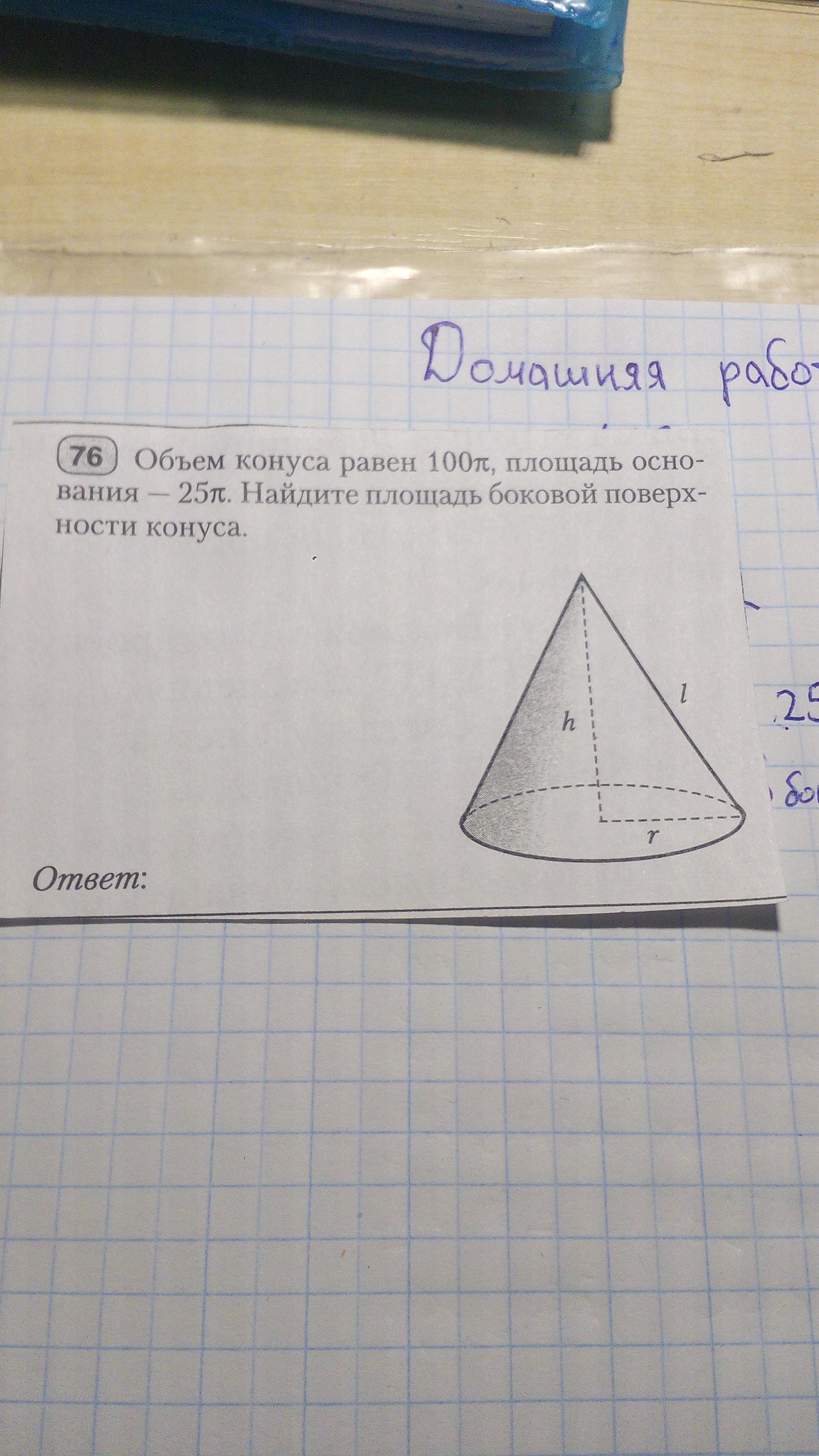

    question img

Ответы 5

  • Спасибо

    • Автор:

      camron
    • 5 лет назад
    • 0
  • Спасибо
  • Пожалуйста!
  • Площадь боковой поверхности конуса вычисляется по формуле s_{bpk} = \pi{rl}где r-радиус основания, l-образующая. Объем конусаv = \frac{1}{3} \pi{ {r}^{2} h}где h-высота конуса. Основанием конуса служит круг и его площадь s_{kr} = \pi{ {r}^{2} }1) Из формулы для площади круга найдем радиус основания:25\pi = \pi {r}^{2} \\ {r}^{2} = 25 \\ r = 52) Из формулы объема конуса найдем высоту конуса100\pi = \frac{1}{3} \pi \times 25h \\ h = \frac{100 \times 3}{25} \\ h = 4 \times3 \\ h = 123) Найдем образующую l по теореме Пифагора из прямоугольного треугольника, у которого катетами являются высота и радиус основания конуса, а гипотенузой - образующая конуса {l}^{2} = {h}^{2} + {r}^{2} \\ {l}^{2} = {12}^{2} + {5}^{2} \\ {l}^{2} = 144 + 25 \\ {l}^{2} = 169 \\ l = 134) Находим площадь боковой поверхности конуса s_{bpk} = \pi \times 5 \times 13 \\ s_{bpk} = 65\pi

  • v=πr²h/3 - объем конуса

    S=πr²=25π⇒r=5 радиус конуса

    v=πr²h/3=100π⇒h=300/r²=300/25=12 высота конуса

    l=√(h²+r²)=√(12²+5²)=13 - образующая конуса

    S=πrl=5*13π=65π≈204,1 - площадь боковой поверхности

  • Добавить свой ответ

Еще вопросы

Топ пользователей

Войти через Google

 или

Забыли пароль?

У меня нет аккаунта, я хочу Зарегистрироваться

How much to ban the user?
1 hour 1 day 100 years