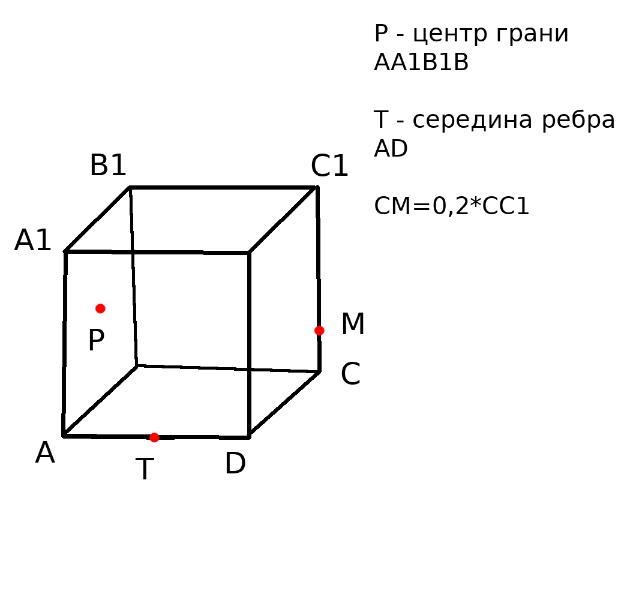
Постройте сечение куба плоскостью, проходящей через точку Р – центр грани AA₁B₁B, точку Т – середину ребра AD и точку М на ребре СС₁, такую что CM = 0,2*CC1. Найдите в каких отношениях сечение делит ребра куба, которые оно пересекает.

Пусть точка Р1 - это проекция точки Р на ребро АВ.

Основой построения является определение положения точки N, принадлежащей плоскости основания куба, как точки пересечения прямых РМ и Р1С.

Далее проводим прямую NT до пересечения с продолжением ребра АВ. Находим точку L, принадлежащую плоскости куба АВВ1А1.

Прямая NL пересекает ребро СД в точке Н.

Через точку Р проводим прямую LP, пересекающую рёбра АА1 и ВВ1 в точках К и Е.

Фигура сечения - пятиугольник ТКЕМН. Это ответ на 1 часть задания.

Для 2 части используются подобные треугольники.

Примем длину ребра куба, равную 10 (для кратности между 1/2 и 1/5).

Вначале находим отрезок EN: P1C = √(5² + 10²) = √125 = 5√5.

2/CN = 5/(5√5 + CN).

5CN =10√5 + 2 CN

CN = 10√5/3.

Далее раскладываем CN на 2 направления сторон основания с учётом соотношения 1/2 в подобном треугольнике Р1ВС

Получаем 10/3 и 20/3.

Следующим определяем длину отрезка AL тоже из подобия:

5/AL = (35/3)/(40/3).    AL = 40/7. Отрезок DН = AL = 40/7.

Теперь переходим к плоскости АВВ1А1.

Аналогично определяем АК = 8/3 и ВЕ = 22/3.

Переходим к ответу на 2 часть задания.

Ребро ВВ1: (8/3)/(22/3) = 8/22 = 4/11.

Ребро АА1: (22/3)/(8/3) = 22/8 = 11/4.

Ребро СД: (30/7)/(40/7) = 30/40 = 3/4.

Остальные 2 ребра даны в задании.