знайдіть площу ромба сторона якого дорівнює 4 см а кут 135 градусів​

Ответ:

8√2 cм²

Пошаговое объяснение:

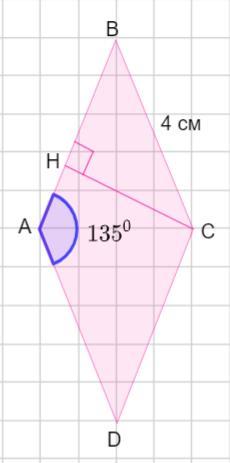
Найти площадь ромба , сторона которого равна 4 см, а угол 135 градусов.

Пусть дан ромб АВСD. У ромба все стороны равны:

АВ =ВС =СD=АD =4 см

∠А =135°.

1 способ

Площадь ромба можно найти по формуле : S =a² · sinα,

где а -сторона ромба, α - угол ромба.

Тогда S =4² · sin135°

sin 135° = sin( 180° - 45°) = sin45° = √2/2

S =16 \cdot \dfrac{\sqrt{2} }{2} =8\sqrt{2}

Значит, площадь ромба равна 8√2 см².

2 способ.

Найдем площадь ромба как произведение стороны ромба на высоту, проведенную к стороне.

Сумма соседних углов ромба равна 180°. Если ∠А = 135°, то

∠В =180° - 135° = 45°.

Проведем высоту ромба СН и рассмотрим ΔСНВ - прямоугольный .

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

sin \angle{} B = \dfrac{CH}{BC} ;\\\\sin45^{0} = \dfrac{CH}{4} ;\\\\ \dfrac{\sqrt{2} }{2} = \dfrac{CH}{4} ;\\\\CH =\dfrac{4\sqrt{2} }{2} =2\sqrt{2}

Тогда высота ромба равна 2√2 см и найдем площадь ромба

S = 4·2√2 = 8√2 cм²

#SPJ1