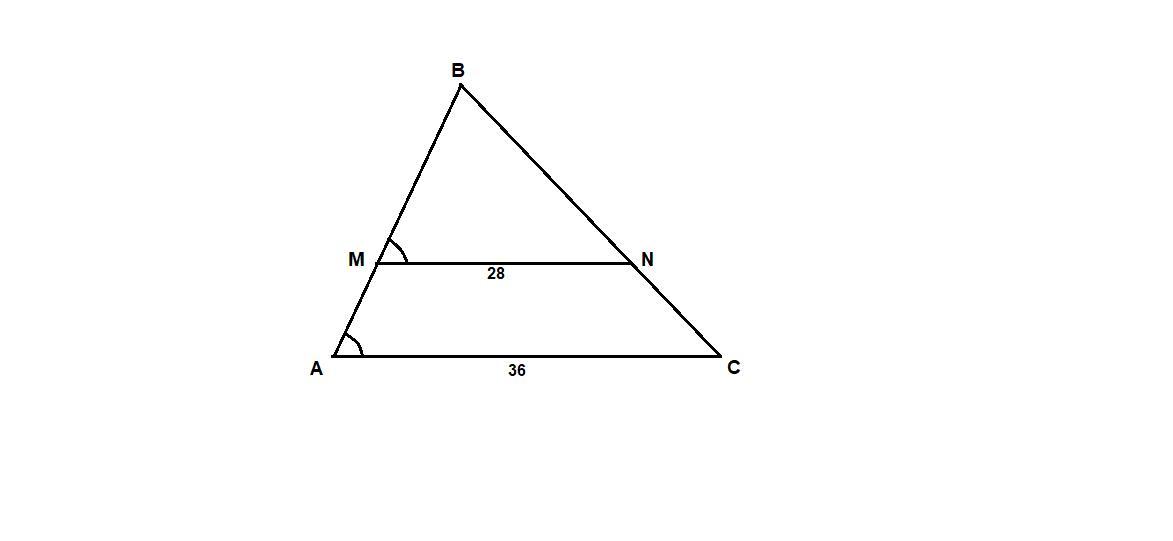
Прямая, параллельная стороне АС треугольника АВС, пересекает стороны АВ и ВС в точках М и N соответственно, АС = 16, MN = 12. Площадь треугольника ABC равна 80. Найдите площадь треугольника MBN.

Ответ:    98 см²

Объяснение:

∠BMN = ∠BAC как соответственные при пересечении параллельных прямых MN и АС секущей АВ,

∠В - общий для треугольников MBN и АВС,   ⇒

ΔMBN подобен ΔАВС по двум углам.

Коэффициент подобия:

k = MN / AC = 28 / 36 = 7/9

Площади подобных треугольников относятся как квадрат коэффициента подобия:

Smbn  / Sabc = k²

Smbn = Sabc · k² = 162  · 49/81 = 98 см²