Площа ромба 144 корень із 2 см, а один із кутів 45°. Точка простору віддалена від уcix сторін ромба на 10 см. Знайдіть відстань від даної точки до площини ромба.​

Ответ:

расстояние от точки до плоскости ромба 8см

Объяснение:

площадь ромба через синус любого угла

S=a²×sinα , отсюда сторона

а=√S/sinα= √(144√2÷sin45°)=√(144√2÷√2/2)=

√(144√2×2/√2)=√144×2=12√2 см

радиус вписанной окружности в ромб

r=S/2a=144√2 /2×12√2=144√2/24√2=144/24=6см

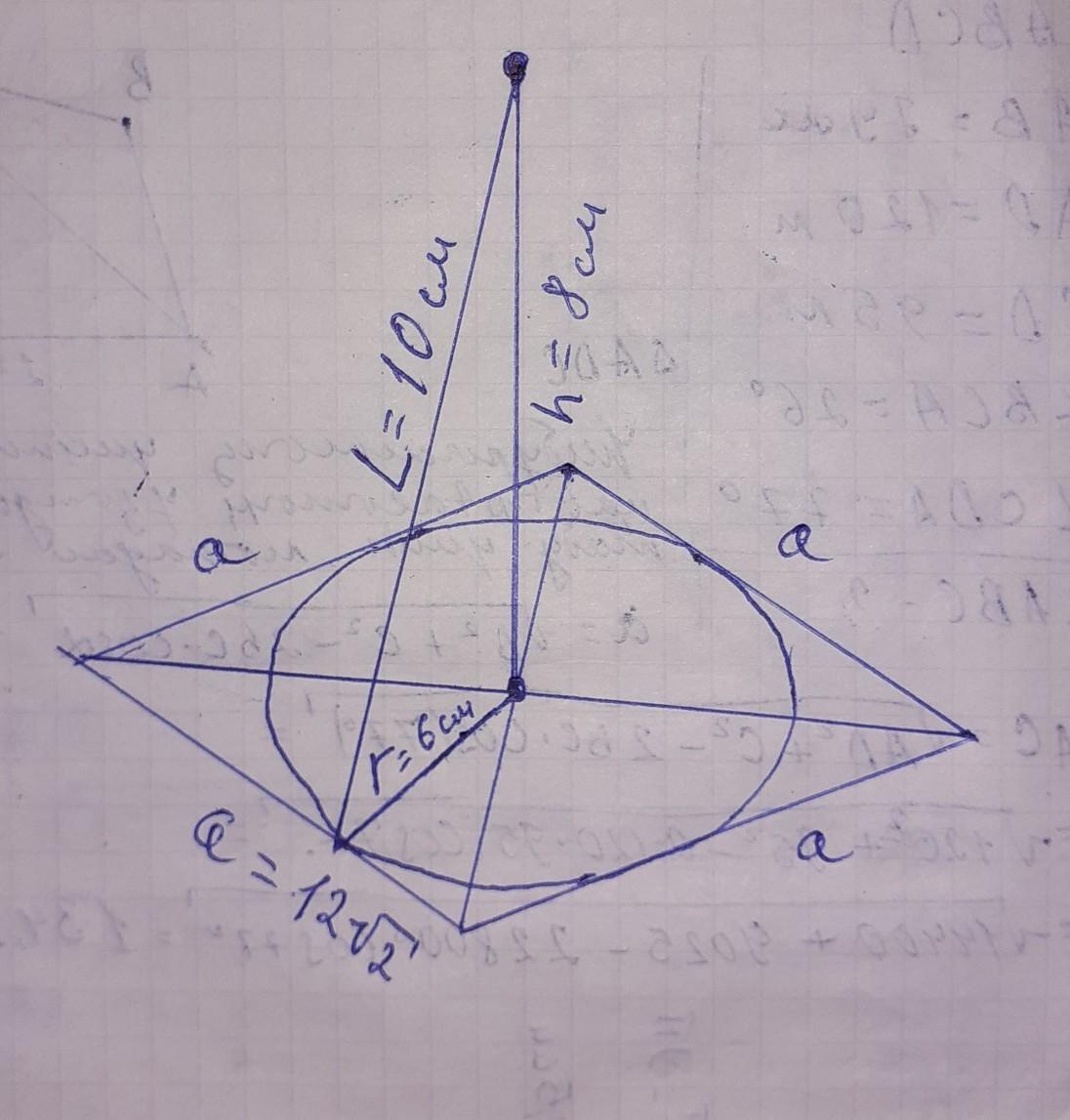
точка находится перпендикулярно к оси пересечения диагоналей ромба, и образует прямоугольный треугольник относительно к оси пересечения диагоналей и одной стороны ромба. где расстояние от точки до стороны ромба является гипотенузой, а радиус вписанной окружности катетом . а неизвестное расстояние от точки до плоскости ромба высотой и вторым катетом.

по теореме Пифагора a²+b²=c²

катет a=r=6см радиус вписанной окружности в ромб,

гипотенуза с=L=10см расстояние от точки до стороны ромба ,

катет b=h высота, расстояние от точки до плоскости ромба ,

находим h=√(L²-r²)=√(10²-6²)=√(100-36)=√64=8см