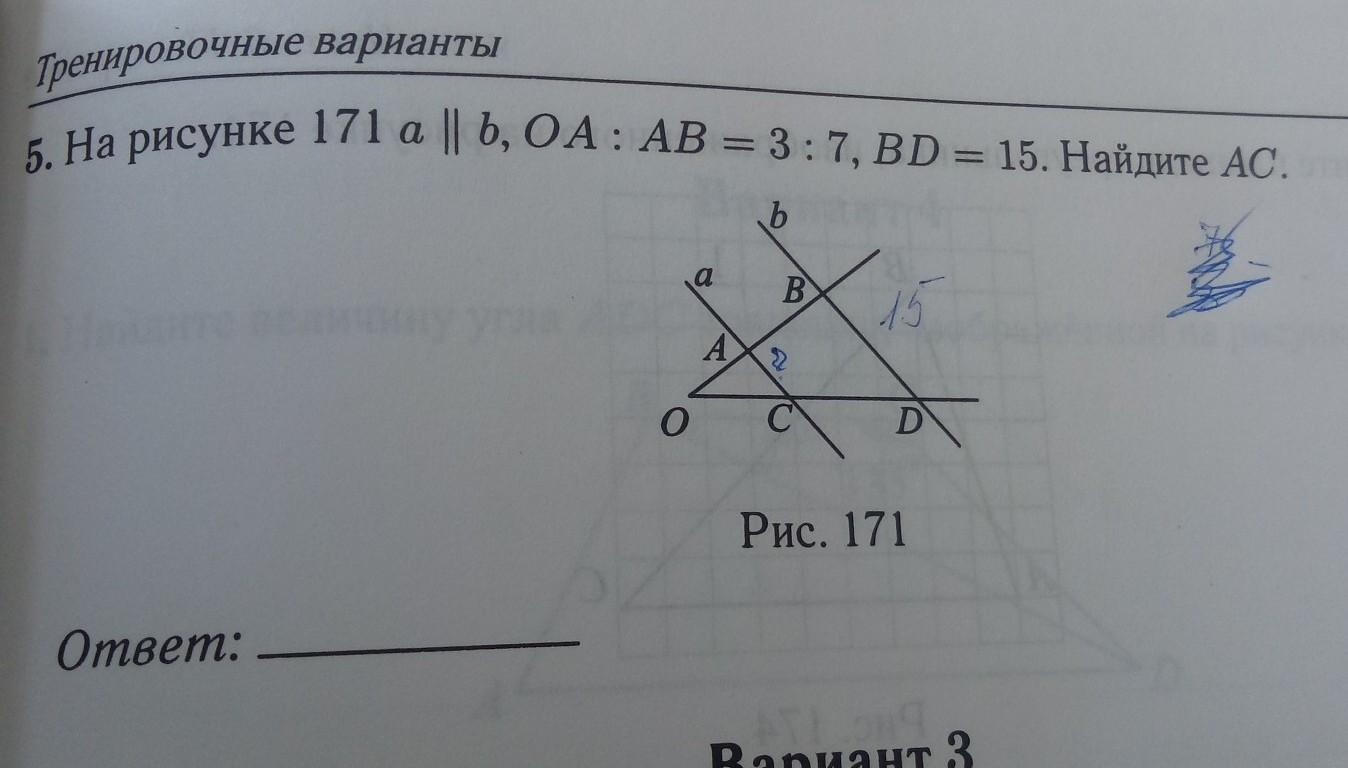
На рисунке 171 a | b, OA: AB = 3:7, BD = 15. Найдите AC.
b
​

Для решения данной задачи, мы можем использовать свойство подобных треугольников и отношение длин соответствующих сторон.

Из условия задачи известно, что OA:AB = 3:7. Это означает, что отношение длин сторон OA и AB равно 3:7.

Также из условия известно, что BD = 15.

Из свойства подобных треугольников, мы знаем, что отношение длин соответствующих сторон подобных треугольников равно.

Так как треугольник ABD подобен треугольнику ABC, мы можем записать отношение длин соответствующих сторон:

AB:BD = AC:CD.

Заменяем известные значения:

7:15 = AC:CD.

Теперь мы знаем отношение AC к CD. 

Также из условия известно, что CD = 171 - AC.

Подставляем это значение в уравнение:

7:15 = AC:(171 - AC).

Мы можем решить это уравнение, чтобы найти значение AC.

Применим правило пропорции:

7 (171 - AC) = 15 AC.

1197 - 7AC = 15AC.

22AC = 1197.

AC = 1197 / 22.

AC ≈ 54.41.

Таким образом, значение AC примерно равно 54.41.