-
1). Вычисли радиус окружности, если отрезок касательной
AK=63√дм и ∢OAK=30°
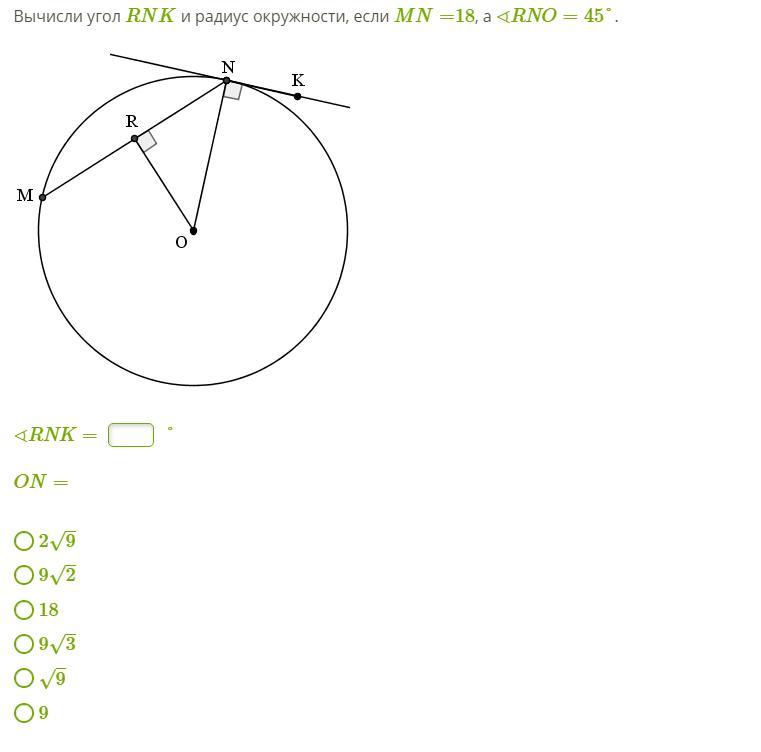
2).Вычисли угол RNK и радиус окружности, если MN= 18, а ∢RNO=45° .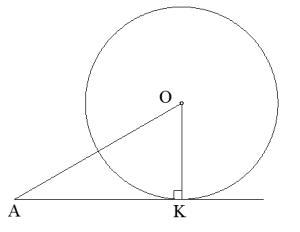
-
Предмет:
Геометрия -
Автор:
rin tin tin - 6 лет назад
-
Ответы 1
-
1) Для вычисления радиуса окружности, зная длину отрезка касательной (AK) и угол OAK, можно использовать теорему тангенсов.
В данном случае, AK = 63√дм и ∢OAK = 30°.
Теорема тангенсов гласит:
tan(∢OAK) = AK / OA
Известно, что tan(30°) = 1/√3.
Таким образом, мы можем записать:
1/√3 = 63√дм / OA
Чтобы найти радиус окружности (OA), перенесем OA в правую часть уравнения и возведем его в квадрат:
OA = 63√дм / (1/√3)
OA = 63√дм √3
OA = 63√3 √дм
OA = 63 √9 √дм
OA = 63 3√дм
OA = 189√дм
Таким образом, радиус окружности (OA) равен 189√дм.
2) Для вычисления угла RNK и радиуса окружности, зная длину отрезка MN и угол RNO, можно использовать синусную теорему и формулу для вычисления радиуса окружности.
В данном случае, MN = 18 и ∢RNO = 45°.
Синусная теорема гласит:
sin(∢RNO) = MN / RN
Зная, что sin(45°) = 1/√2, и подставив известные значения, можем записать:
1/√2 = 18 / RN
Перенесем RN в правую часть уравнения и выразим его:
RN = 18 / (1/√2)
RN = 18 √2
RN = 18√2
Таким образом, длина отрезка RN равна 18√2.
Чтобы вычислить угол RNK, воспользуемся свойством касательной, согласно которому угол между касательной и радиусом окружности, проведенным к точке касания, равен 90°.
Таким образом, угол RNK равен 90°.
Для вычисления радиуса окружности (RK), воспользуемся формулой для радиуса окружности, которая связывает радиус, длину отрезка и угол:
RK = RN / sin(∢RNK)
Ранее мы нашли, что RN = 18√2. Заменяем значения:
RK = 18√2 / sin(90°)
RK = 18√2 / 1
RK = 18√2
Таким образом, радиус окружности (RK) также равен 18√2.
-
Автор:
Fedoseewa27 - 2 года назад
-
0
-
-
Добавить свой ответ
-
Помогите пожалуйста задания по физике срочно!!!!
-
Предмет:
Физика -
Автор:
diet cokepdwr - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Сравнить излучение абсолютно тёплое тело при температуре t1=100°c,t2=0°c
-
Предмет:
Астрономия -
Автор:
hannacortez - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Пожалуйста, помогите, возможно у кого-то есть кроссворд по географии на тему "Народы мира"? 25 слов
-
Предмет:
География -
Автор:
pickleadm4 - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
что такое топографическое изображение?
-
Предмет:
Другие предметы -
Автор:
allieemml - 6 лет назад
-
Ответов:
6 -
Смотреть
-
