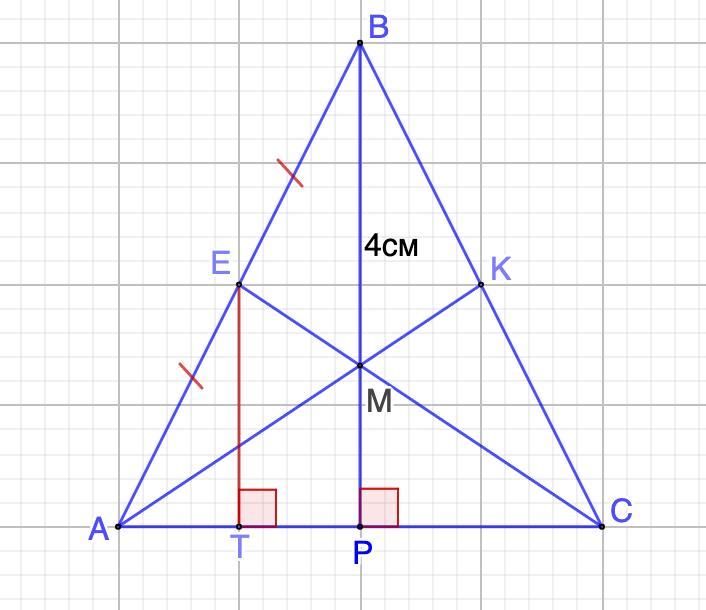
медіани рівнобедреного трикутника АВС (АВ=ВС) перетинаються в точці М. Відомо, що ВМ=4 см. Знайти відстань від середини сторони АВ я до сторони АС.

Ответ:

3 см.

Пошаговое объяснение:

Дано: ΔАВС - равнобедренный.

АВ = ВС;

АК, ВР, СЕ - медианы.

ВМ = 4 см.

ЕТ ⊥ АС

Найти: ЕТ.

Решение:

Рассмотрим ΔАВС.

• Медианы треугольника пересекаются в одной точке и делятся точкой пересечения в отношении 2 : 1, начиная от вершины.

⇒ ВМ : МР = 2 : 1.

Пусть МР = х см ⇒ ВМ = 2х см.

2х = 4

х = 2

⇒ МР = 2 см; ВМ = 4 см; ВР = 6 см.

2. Рассмотрим ΔАВР.

• В равнобедренном треугольнике медиана, проведенная к основанию, является высотой.

⇒ ВР ⊥ АС.

ЕТ ⊥ АС (по условию)

• Если две прямые перпендикулярны третьей, то они параллельны между собой.

⇒ ЕТ || ВР.

АЕ = ЕВ (СЕ - медиана)

• Признак средней линии треугольника: если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей — этот отрезок можно назвать средней линией этого треугольника.

⇒ ЕТ - средняя линия ΔАВР.

• Средняя линия параллельна одной из сторон треугольника и равна ее половине.

⇒ ЕТ = ВР : 2 = 6 : 2 = 3 (см)