-
Помогите по геометрии пожалуйста срочно нодо
В окружность вписан квадрат со стороной 8 см (см. рис.). Определите площадь закрашенной части.
Screenshot_1.png
Задание 3.
Окружность вписана в правильный шестиугольник со стороной 8 см. K, L, M, N, O, P – точки касания. Определите длину дуги KLM.
Screenshot_2.png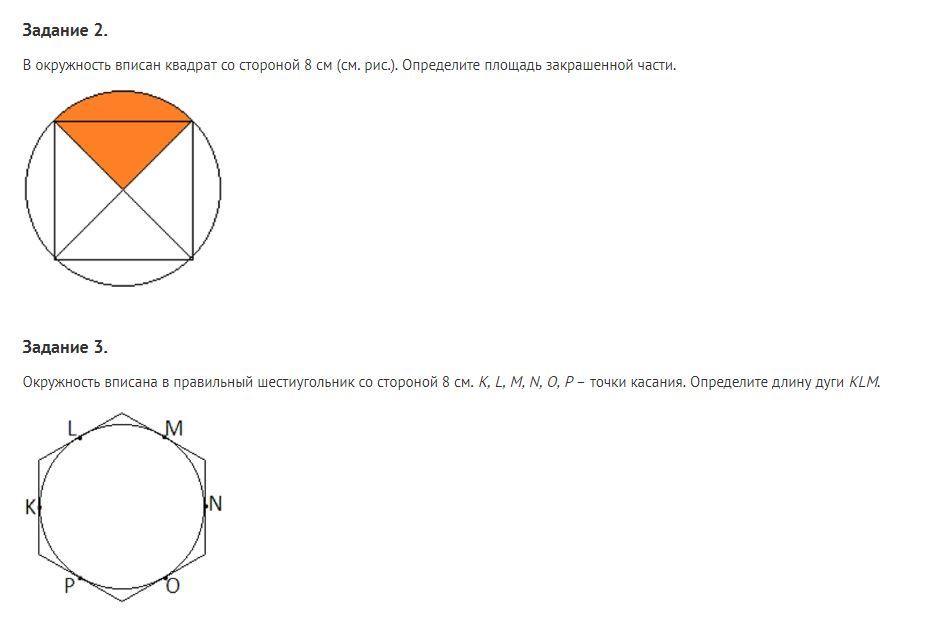
Ответы 1
-
Для решения этой задачи, нам понадобится знание о свойствах правильного шестиугольника и вписанной окружности.
В правильном шестиугольнике, каждый угол равен 120 градусам, а длина стороны равна 8 см. Точки касания окружности с сторонами шестиугольника делят каждую сторону на две равные части.
Таким образом, дуга KLM является третью частью окружности, вписанной в шестиугольник. Поскольку окружность имеет длину 2πr, где r - радиус окружности, длина дуги KLM составляет 1/3 от общей длины окружности.
Радиус окружности можно найти, используя формулу r = a/2√3, где a - длина стороны шестиугольника. В данном случае, a = 8 см, поэтому радиус r = 8/2√3 = (4√3)/3 см.
Теперь мы можем найти длину дуги KLM, используя формулу длины окружности: длина дуги = (1/3) 2πr.
Длина дуги KLM = (1/3) 2 π (4√3)/3 = (8√3π)/9 см.
Таким образом, длина дуги KLM составляет (8√3π)/9 см.
-
Автор:
Fedoseewa27 - 2 года назад
-
0
-
-
Добавить свой ответ
-
1.Чём вы объясните распространение кальвинизма в Европе?
2.В каких странах распростронился в первую очередь кальвинизм?
3.Почему именно буржуазии выбрала кальвинизм себе вероучением?
2 задание
Определите верное или неверное утверждение.
1. Рафаэль санти - автор книги мона лиза (да/нет)
2. Требование "дёшевой церкви" - одна из причин реформации (да/нет)
3. Гумманисты выступали за подчинение католической церкви (да/нет)
4. Томас Мюнцер - вождь крестьянского восстания в Швейцарии (да/нет)
5. Галилео Галилей с помощью телескопа открыл новые звезды (да/нет)
Заранее спасибо огромное!!!! -
помогите, даю 30 баллов
найдите 3 способа решения данного уравнения
2х + 7у = 10 (сделайте решение пж)
решите системы уравнения
и 3 задание-
Предмет:
Математика -
Автор:
bud8p4a - 6 лет назад
-
Ответов:
3 -
Смотреть
-
-
Помогите мне пожалуйста (все написать) 1) Почву отпустили в стакан с водой.Из почвы выходят ________,значит в ней есть воздух.2)Почву нагрели.На блюдце появились ______,значит в почве есть _________.3)Воду из стакана нагрели,она испарилась.На стекле остались ______,значит в почве есть ___________.4)Почва в воде отстоялась.Ты видишь,что в ней есть разные __________.
Помогите пожалуйста СРОЧНО дам 34 балла-
Предмет:
Другие предметы -
Автор:
aires - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
пожалуйста, напишите юмористический рассказ. очень срочно.
-
Предмет:
Литература -
Автор:
drake83 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
