-
помогите плз !!!!!!!!!!!!!!!!!!!!!!
Серединные перпендикуляры к сторонам AB и BC треугольника ABC пересекаются в точке M, которая принадлежит стороне AC. Докажите, что точка M — середина отрезка AC.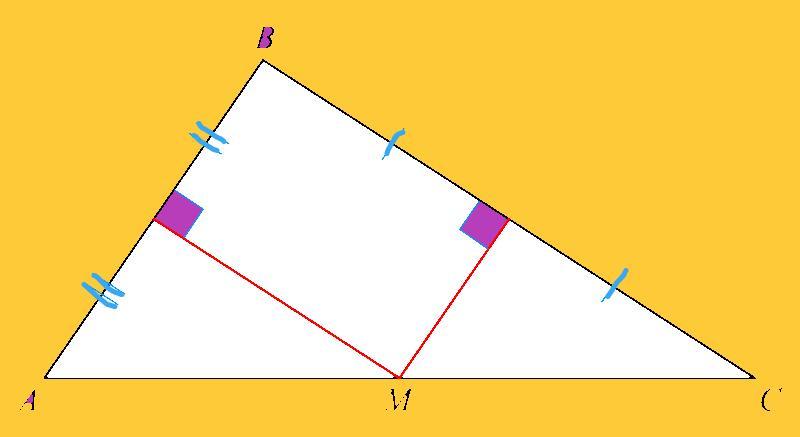
-
Предмет:
Геометрия -
Автор:
porfiriorobbins - 6 лет назад
-
Ответы 3
-
Благодарю за решение
-
Автор:
bebe73 - 6 лет назад
-
0
-
-
Рассмотрим прямоугольник HBKM (допустим).
ВК = НМ; НВ=КМ
Рассмотрим треугольник АНМ и МКС
МК=НВ, а АН=НВ (по условию), тогда МК=АН
ВК = НМ, а КС=ВК (по условию), тогда КС=НМ
углы АНМ=МКС, следовательно треугольники равны, значит все их элементы также равны. От суда следует, что гипотенузы АМ и МС равны, значит точка М — середина отрезка AC, что и требовалось доказать
-
Автор:
katelynjames - 6 лет назад
-
0
-
-
Точка М (пересечение серединных перпендикуляров) является центром окружности описанной вокруг данного треугольника. Следовательно АМ и МС радиусы и они равны.
-
Автор:
axel3 - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Помогоите log3 4 - log3 324
-
Предмет:
Математика -
Автор:
arturoulab - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
в каких случаях совершается работа? 1) шарик катится по гладкому горизонтальному столу 2) кирпич лежит на земле 3) автопогрузчик поднимает груз
-
Предмет:
Физика -
Автор:
giannigfsm - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Кілька книжок на 1 полиці,у тричі більше ніж на 2. Якщо з 1 полиці взяти 8 книжок,а на 2 поставити 2 книжки,то на 1 полиці стане у 2 рази більше книжок,ніж на 2 полиці. Скільки книжок на кожній полиці?
Помогите пж! Очень срочно!-
Предмет:
Математика -
Автор:
macintoshroy - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Одну сторону прямоугольника увеличили на 40%,а другую уменьшили на 70%.Как изменилась площадь прямоугольника и на сколько процентов? РЕШИТЕ ПЛИЗ
-
Предмет:
Математика -
Автор:
patricia8 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
