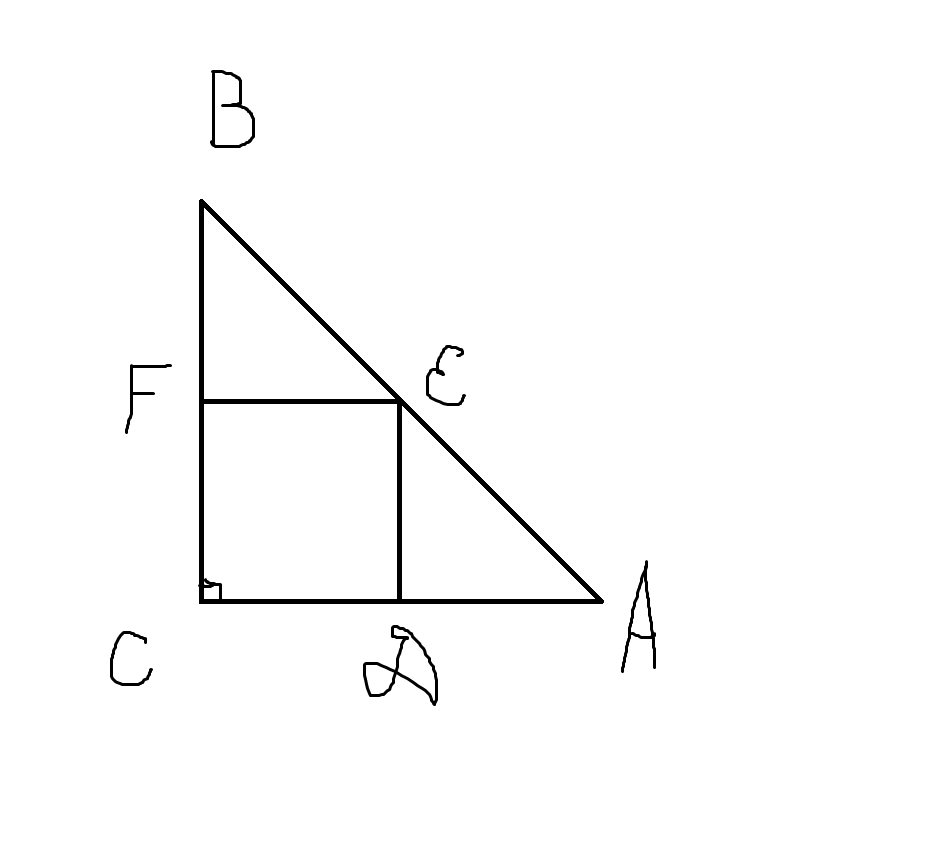
Даны равнобедренный прямоугольный треугольник АВС с прямым углом С, катетом АС=12 см и квадрат CDEF, такой, что две его стороны лежат на катетах, а его вершина Е на гипотенузе треугольника.Найдите периметр квадрата CDEF.

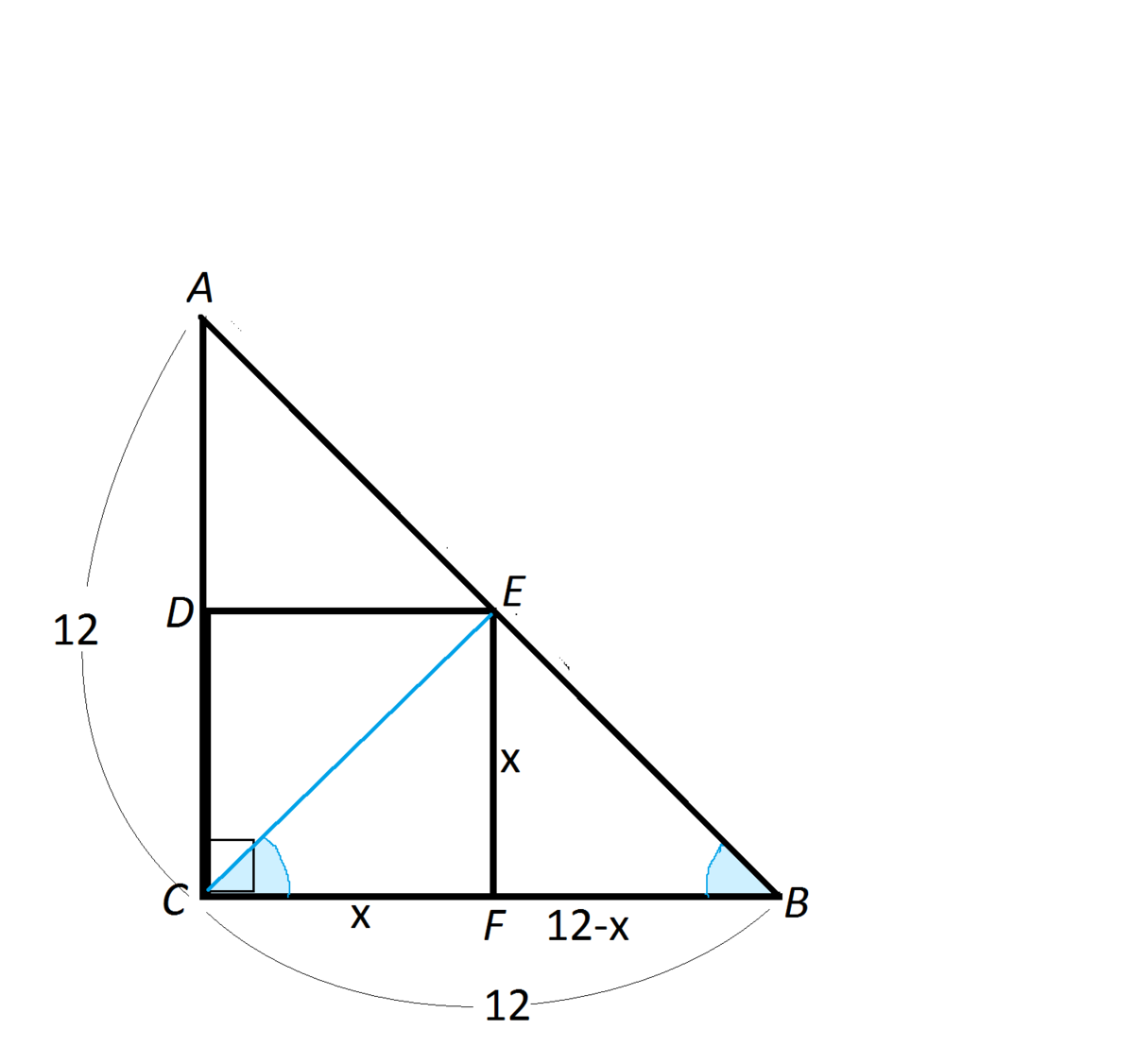
Способ 1)Проведем диагональ квадрата СЕ. В треугольнике ВЕС углы при основании СВ равны 45°.Этот треугольник равнобедренный.Высота ЕF является его медианой и делит ВС на две равные части. х=ВС:2=12:2=6Периметр равен 4*6=24 смСпособ 2)Треугольники FBE  и АВС  подобны, т.к. оба прямоугольные и имеют общий угол.Пусть сторона квадрата равна хТогда ВF=12-хИз подобия треугольников вытекает отношение АС:EF=BC:FB12:х=12:(12-x)12х=144-12х24х=144х=144:24=6Периметр равен 4*6=24 см