-
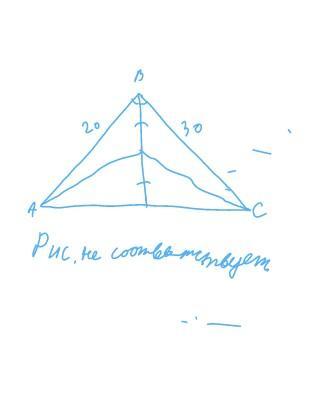
Точка M — середина биссектрисы AL треугольника ABC. Известно, что AB=20, AC=30, а площадь треугольника ABM равна 30. Найдите площадь треугольника MLC
Ответы 1
-
По теореме о биссектрисе
BL/CL =AB/AC =20/30 =2/3
Треугольники BAL и CAL имеют общую высоту (перпендикуляр из вершины A к BC), следовательно их площади относятся как основания.
S(BAL)/S(CAL) =BL/CL =2/3
Треугольники ABM и MBL имеют общую высоту и равные основания (AM=ML), следовательно их площади равны.
S(ABM)=S(MBL)
Аналогично S(AСM)=S(MСL)
S(BAL)= 2 S(ABM)
S(CAL)= 3/2 S(BAL)
S(MCL)= 1/2 S(CAL) =1/2 *3/2 *2 *30 =45

-
Автор:
fischer - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
- доказать тождество 1+tg^2a=1/cos^2a. Помогите.
-
Чем внешне жильные породы отличаются от интрузивных и эффузивных пород?
-
Предмет:
География -
Автор:
celinaq0ol - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Независимые страны зарубежной Европы
Сколько и какие -
К глаголам 1 спряжения подберите и запишите синонимы к глаголам 2 спряжения антонимы хохочет,помнит,ловит,танцует,размышляет,просит, наблюдает,фантазирует,мечтает,кричит,уходишь.-
Предмет:
Русский язык -
Автор:
biggiehkh4 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
