-
На стороне BC треугольника ABC выбрана точка M. Биссектрисы углов B и C пересекают отрезок AM в точках K и L соответственно. Известные длины отрезков изображены на рисунке. Найдите отношение площади треугольника BKM к площади треугольника CLM.
Срочно пж
Заранее благодарю.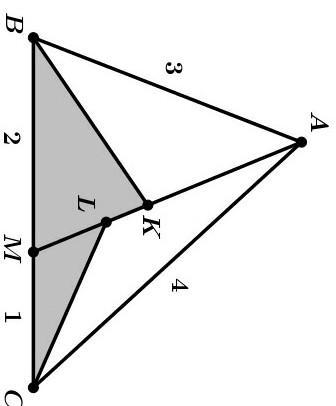
Ответы 1
-
Ответ: 4/1.
Объяснение:
По свойству биссектрисы треугольника имеем:
AK/KM = AB/BM = 3/2,
AL/LM = AC/CM = 4/1,
Кроме того:
S(ABK)/S(BKM) = (0,5*h*AK)/(0,5*h*KM) = AK/KM = 3/2,
то есть S(ABK) = (3/2)*S(BKM).
S(ACL)/S(CLM) = (0,5*h*AL)/(0,5*h*LM) = AL/LM = 4/1 = 4,
то есть S(ACL) = 4*S(CLM),
S(ABM)/S(ACM) = (0,5*h*BM)/(0,5*h*CM) = BM/CM = 2/1 = 2.
Кроме того: S(ABM) = S(ABK) + S(BKM)
S(ACM) = S(ACL) + S(CLM),
поэтому
( S(ABK) + S(BKM) )/( S(ACL) + S(CLM) ) = 2,
( (3/2)*S(BKM) + S(BKM) )/( 4*S(CLM) + S(CLM) ) = 2,
( (5/2)*S(BKM) )/( 5*S(CLM) ) = 2,
( (1/2)*S(BKM) )/S(CLM) = 2,
S(BKM)/S(CLM) = 2*2 = 4.
-
Автор:
bishop - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
помогите пожалуйста написать письмо другу про страну Турцию на английском и написать 5 мест в Турции
-
Предмет:
Английский язык -
Автор:
mercle - 6 лет назад
-
Ответов:
6 -
Смотреть
-
-
избавиться от иррациональности в знаменателе:
4/√5-√3 -
В двух бочках вместе 912 л бензина. Когда из первой бочки взяли 1/5 бензина, а из второй бочки взяли 3/7 бензина, то в обеих бочках бензина стало поровну.
Сколько литров бензина было в каждой бочке первоначально?
Ответ:
в первой бочке было первоначально
л бензина;
во второй бочке было первоначально
л бензина.-
Предмет:
Математика -
Автор:
nieves - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
найдите длину третьей стороны равнобедренного треугольника, если длины равных сторон 9,6 дм а периметр 28,1 дм
-
Предмет:
Математика -
Автор:
bugseypatel - 6 лет назад
-
Ответов:
4 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
