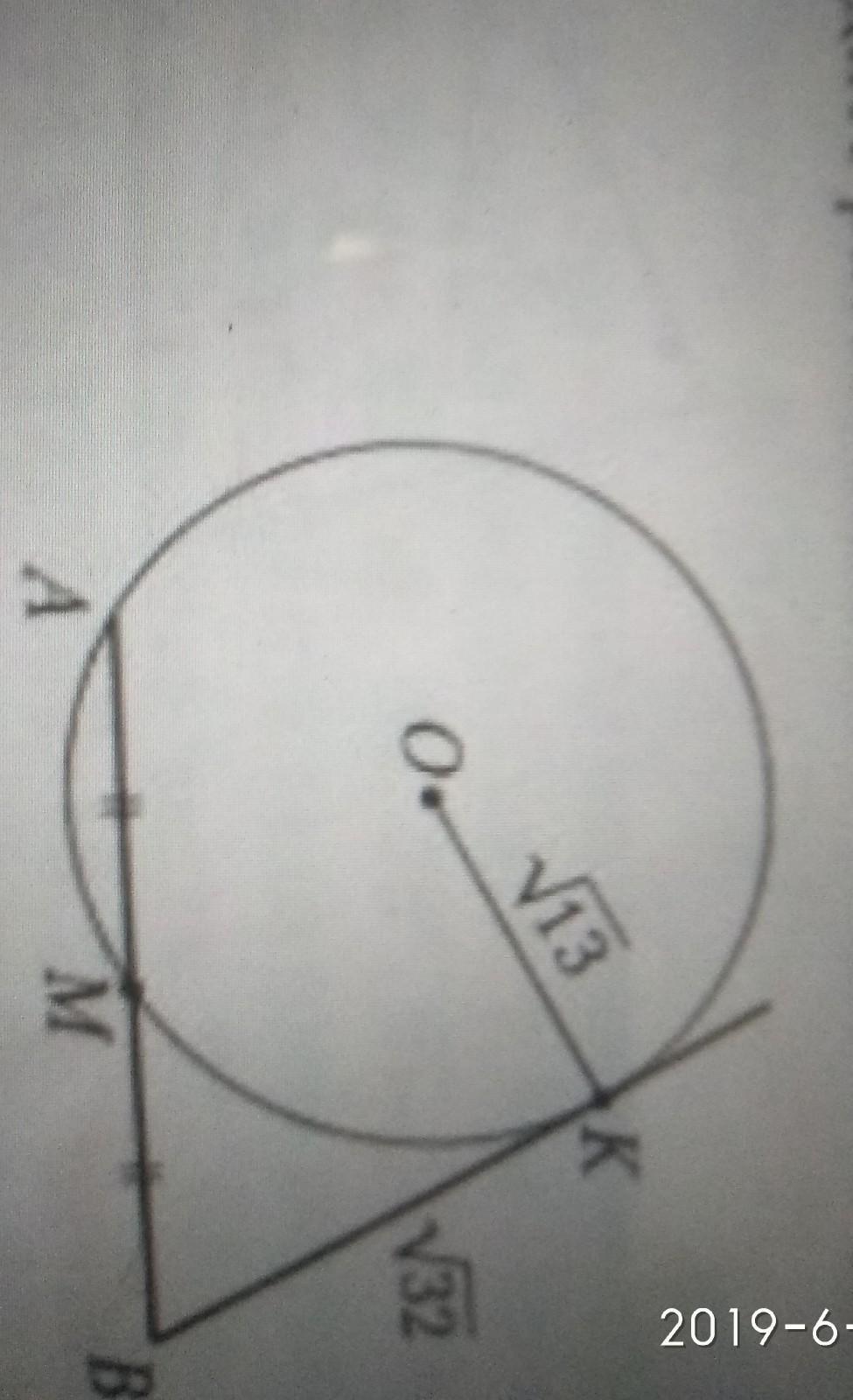
Помогите пожалуйста, дам много баллов))))​ Найти расстояние от точки O до AB

мне расстояние от точки O до AB

тогда к отрезку ВМ опускаем перпендикуляр ОН .НМ=1/2ВМ=4:2=2 см.По теореме Пифагора находим ОН=корень квадратный ОМ ^2-HM^2=корень квадратный 13-4=корень квадратный из 9=3 см-расстояние от точки O до AB.

А ну ладно, спс

Извини по невнимательности не дорешала

Дорешайте, пожалуйста.

Ответ:

Объяснение:

Дано:ВК-касательная,ВА-секущая окружности (О,г) ,ОК=√13,КВ=√32,ВМ=МА

Найти:длину секущей АВ

Из свойств секущей и касательной известно:

ВК²=ВМ*АВ

ВМ принимаем за х,тогда АВ=2х,так как ВМ=МА по условию.

ВК²=2х*х

(√32)²=2х²

32=2х²

х²=32:2

х²=16 см

х=√16=4 см-ВМ

Тогда к отрезку ВМ опускаем перпендикуляр ОН .НМ=1/2ВМ=4:2=2 см.По теореме Пифагора находим ОН:

ОН=√ ОМ ²-HM²=√(√13)²-2²=√ 13-4=√9=3 см-расстояние от точки O до  АВ.