-
пожалуйста, помогите
очень срочнооооооо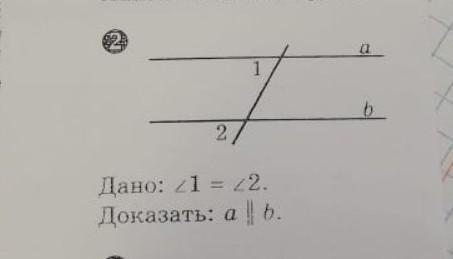
-
Предмет:
Геометрия -
Автор:
leilaniuwbl - 6 лет назад
-
Ответы 1
-
Объяснение:
Воспользуемся методом от противного. Пусть накрест лежащие углы равны, но предложенные прямые не параллельны. Если прямые не параллельны, то они пересекутся в одной точке. На чертеже секущая c пересекает прямые a и b в точках A и B, а сами прямые пересекаются в точке C.
В результате образуется треугольник ABC, у которого угол при вершине B равен внешнему углу при вершине A. Это дано по условию: были даны равные углы при секущей.
Сумма углов в треугольнике равна 180°. Если угол треугольника при вершине B равен x градусов, то два остальных угла треугольника в сумме равны 180 – x.
Так как угол B треугольника равен внешнему углу A, то значит A также равен x градусов. Внутренний угол A и внешний угол A треугольника в сумме составляют 180°, так как это смежные углы. Тогда мы получаем, что внутренний угол A треугольника равен 180 – x. Но этого быть не может, так как 180 – x является суммой углов A и C треугольника.
Такое может быть только в случае, если угол C треугольника равен 0°. Однако такого быть не может, так как в этом случае отрезки AC и BC наложились бы друг на друга. То есть прямая a совпала бы с прямой b. Однако по условию даны разные прямые.
Таким образом доказано, что если накрест лежащие углы равны, то прямые пересекаться не могут. А если прямые не имеют точек пересечения, то они параллельны.
-
Автор:
hank - 6 лет назад
-
0
-
-
Добавить свой ответ
-
Помогите пожалуйста.
[tex]\sqrt{\frac{2sin^{2}x}{3cos x+3}=1 }[/tex]
Найти все корни уравнения на отрезке [0; 2[tex]\pi[/tex]]
p.s. Подробно прорешать.-
Предмет:
Алгебра -
Автор:
tobiasbk8n - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
1) Рассчитайте вес тела массой 75кг
2)Рассчитайте молярную массу Н2РО4
3)При деформации изгиба .....
4)Чему равна абсолютная температура, которая соответствует 63 градуса цельсия?
5) При адиабатном процессе внешние силы совершают работу 200Дж. Какое количество теплоты получает газ?-
Предмет:
Математика -
Автор:
octaviokbe6 - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
George suggested ..... to historical places
A)Went
B)to go
C)going
D)goes
С объяснением-
Предмет:
Английский язык -
Автор:
moralesjvkw - 6 лет назад
-
Ответов:
2 -
Смотреть
-
-
What ... you ... at that time yesterday?
A)were,doing
B)have,done
C)do,do
D)will do-
Предмет:
Английский язык -
Автор:
sheena - 6 лет назад
-
Ответов:
3 -
Смотреть
-
