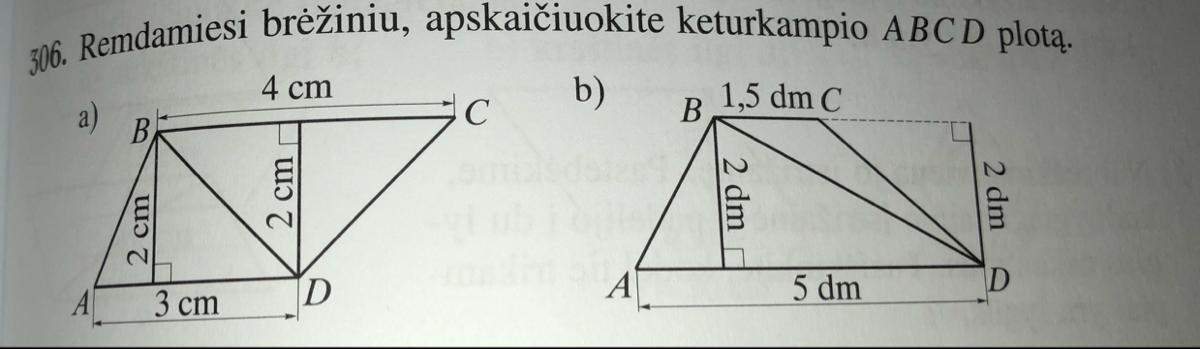
смотря на рисунок высчитайте площадь четырехугольника A B C D

Площадь трапеции равна произведению полусуммы оснований на высоту

a) В ΔBDE (DE - перпендикуляр к BC) и ΔBHB (BH - перпендикуляр к AD)

BD - общая

BH = DE (условие)

Угол DEB в ΔBDE и угол BHD в ΔDHB равны по 90°, значит по теореме пифагора BE^2 = BD^2 - DE^2

и DH^2 = BD^2 - BH^2

BH = DE

DH^2 = BD^2 - BH^2

BE^2 = BD^2 - BH^2

DH = BE

След - но, ΔBHD = ΔDEB (по трём сторонам)

Значит, угол BDA = угол DBC

BD - секущая, значит BC ll AD

След-но ABCD - трапеция

1-ое основание - AD = 3 см, 2-ое основание - BC = 4 см, высота BH = 2 см

S(ABCD) = (AD + BC) × BH/2 = 7 × 2/2 =

Ответ : 7 см^2

b) В ΔBDE (DE - перпендикуляр к BC) и ΔDBH (BH - перпендикуляр к AD)

BD - общая

BH = DE (условие)

Угол DEB в ΔBDE и угол BHD в ΔDBH равны по 90°, значит по теореме пифагора BE^2 = BD^2 - DE^2

и DH^2 = BD^2 - BH^2

BH = DE

DH^2 = BD^2 - BH^2

BE^2 = BD^2 - BH^2

DH = BE

След - но, ΔBHD = ΔDEB (по трём сторонам)

Значит, угол BDA = угол DBC

BD - секущая, значит BC ll AD

След-но ABCD - трапеция

1-ое основание - AD = 5 дм, 2-ое основание - BC = 1,5 дм, высота BH = 2 дм

S(ABCD) = (AD + BC) × BH/2 = 6,5 × 2/2 = 6,5 дм^2 (650 см^2)

Ответ : 6,5 дм^2 (650 см^2)