ПОМОГИТЕ ПОЖАЛУЙСТА ОТДАМ ВСЕ БАЛЛЫ ЧТО ЕСТЬ !!!!ПОМОГИТЕ

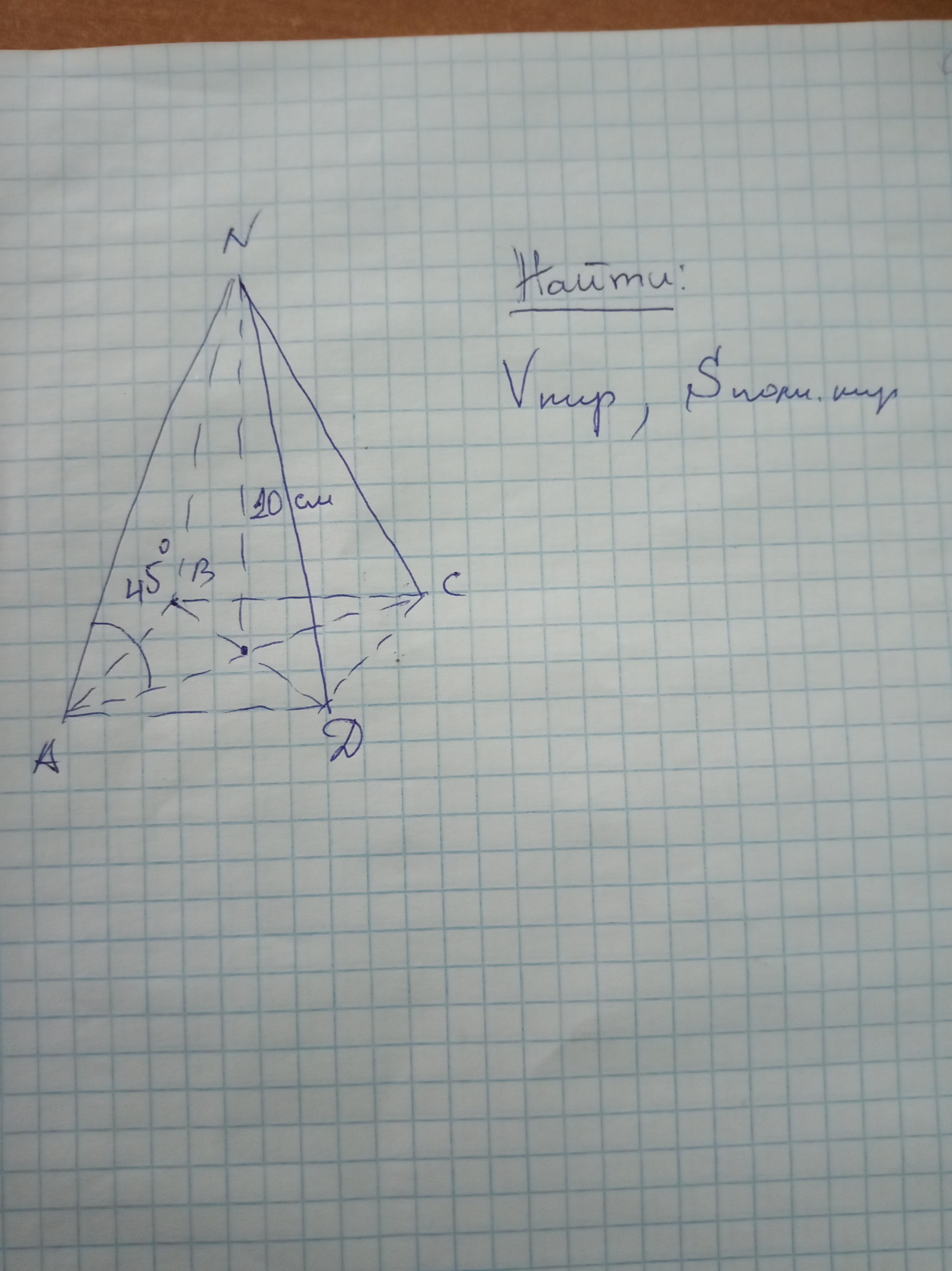
Дана правильная пирамида, боковое ребро которой наклонено к плоскости основания под  углом 45°, с высотой NО=10см, т.к. АО- проекция АN на плоскость основания, то ∠NАО=45°. ΔNАО- равнобедренный,т.к. и второй угол в нем ∠N=45°, значит, АО=NО=10, тогда диагональ квадрата АС=2*10=20/см/, а сторона квадрата АД*√2/2=10√2/см/, Площадь квадрата равна АС²/2=400/2=200/см²/, объем пирамиды равен трети произведения площади основания на высоту, т.е. 200*10/3=2000/3/см³/.

Чтобы найти площадь боковой поверхности, надо найти площадь

ΔАNВ  и учетверить ее. Найдем площадь по формуле Герона.

АN=√(АО²+ОN²)=√(100+100)=10√2/см/; Полупериметр равен

(10√2+10√2+10)/2=10√2+5, площадь равна

√((10√2+5)(10√2-5)*5*5)=5√(200-25)=5√175=5*5√7=25√7/см²/, тогда площадь боковой поверхности равна 4*25√7=100√7/см²/, а площадь полной поверхности (100√7+200)/см²/