-
Решить легкую стереометрическую задачку на 98 баллов.
Доказать что отношение площади основания к площади полной поверхности у описанной пирамиды=
[tex]\frac{S_o_s_n}{S_p_o_l_n}=\frac{cos(\alpha)}{1+cos(\alpha)}[/tex]
Где α- угол между боковой гранью и плоскостью основания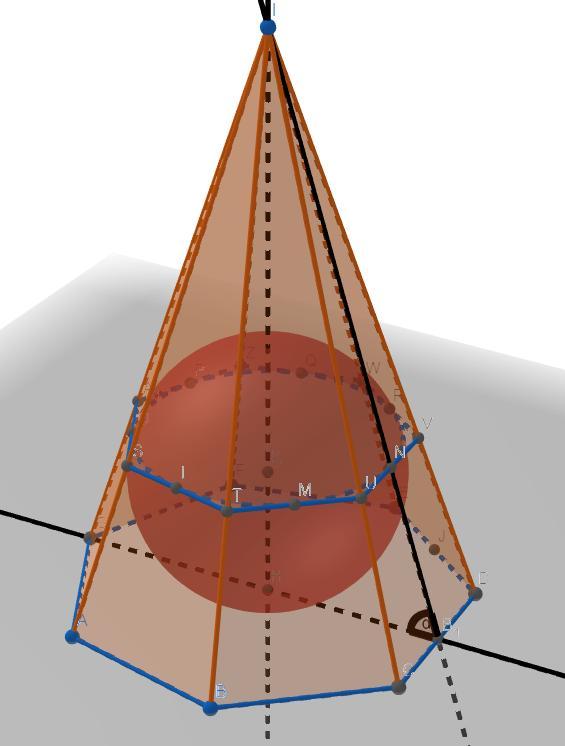
Ответы 6
-
я доказывал через объёмы, но так тоже очень хорошо
-
Автор:
orestesgkb4 - 6 лет назад
-
0
-
-
Можно отметить, что cosa = S осн. / S бок.
-
Автор:
oseas - 6 лет назад
-
0
-
-
Здравствуйте, можете помочь с алгеброй?
-
Автор:
luke56 - 6 лет назад
-
0
-
-
Здравствуйте, можете помочь с алгеброй?
-
Автор:
alivia - 6 лет назад
-
0
-
-
Доказательство:Если в пирамиду вписан шар, то вершина данной пирамиды проецируется в точку пересечения биссектрис основания, а боковые грани наклонены к основанию под одним и тем углом. Рассмотрим произвольную пирамиду MABC. Пусть r - радиус вписанной окружности в ΔАВС, тогда ОК = ОТ = ОН = rВ ΔМОТ: cosα = OT/MT ⇒ MT = r/cosαS бок.пов. = (1/2) • P • h = p • MT = p•r/cosαS осн. = р • r
Доказано

-
Автор:
bridgettejimenez - 6 лет назад
-
0
-
-
В пирамиду вписан шар - все боковые грани под углом a к плоскости основания.
O - основание перпендикуляра из вершины S.
S(A1OA2) = S(A1SA2) cosa (площадь ортогональной проекции)
Проекции боковых граней покрывают основание.
S осн = S(A1OA2) + S(A2OA3) + ...
S бок = S(A1SA2) + S(A2SA3) + ...
S осн /S бок = cosa
S полн /S осн = (S осн +S бок)/S осн = 1 + 1/cosa

-
Автор:
phantomtr9o - 6 лет назад
-
0
-
-
Добавить свой ответ
Еще вопросы
-
Мастер и Маргарита, перескажите о чем это произведение своими словами и желательно по-тупее
-
Предмет:
Литература -
Автор:
clydesims - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
Какое положительное влияние человека на животных вам известно?
-
Предмет:
Биология -
Автор:
amirahnielsen - 6 лет назад
-
Ответов:
1 -
Смотреть
-
-
В корзине лежат яблоки красного и зеленого
цветов, красного - 10 штук. Известно, что
вероятность вытащить яблоко зеленого
цвета, не глядя в корзину, равняется 0,75.
Сколько всего яблок в корзине? -
3. Найдите область определения функции:
14х-25
6x2+x-1-
Предмет:
Математика -
Автор:
abigailvx9z - 6 лет назад
-
Ответов:
5 -
Смотреть
-
How much to ban the user?
1 hour
1 day
100 years
