-
Дано: EBCD-трапеция AD=15
Найти:PEBCD (периметр EBCD)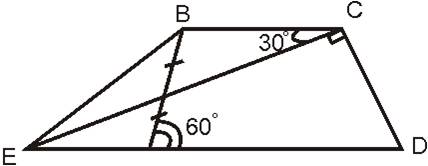
-
Предмет:
Геометрия -
Автор:
malakaidelacruz - 6 лет назад
-
Ответы 1
-
Ответ:
15/4 · (√7 + 7)
Объяснение:
∠CED = ∠BCE = 30° как накрест лежащие при пересечении ED║BC секущей ЕС.
ΔCED: ∠ECD = 90°, ∠CED = 30° ⇒ ∠ CDE = 60°,
CD = 1/2 ED = 15/2,
EC = ED · sin∠CDE = 15 · √3/2 = 15√3/2.
Трапеция ABCD равнобедренная, так как углы при основании равны (∠CDA = ∠BAD = 60°), значит АВ = CD = 15/2.
Так как трапеция АВСD равнобедренная, то
∠ABC = ∠DCB = 90° + 30° = 120°.
ΔMBC: ∠MBC = 120°, ∠BCM = 30°, ⇒ ∠BMC = 30°,
значит треугольник равнобедренный,
ВМ = ВС = 1/2 АВ = 15/4.
Найдем ЕВ из треугольника ЕВС по теореме косинусов:
EB² = BC² + EC² - 2 · BC · EC · cos∠BCE
EB² = (15/4)² + (15√3/2)² - 2 · 15/4 · 15√3/2 · √3/2
EB² = 225/16 + 225 · 3 / 4 - 225 · 3 / 8 =
= 225/16 + 225 · 3 / 8 = 225 · 7 / 16
EB = 15√7/4
Pebcd = EB + BC + CD + ED =
= 15√7/4 + 15/4 + 15/2 + 15 =
= 15√7/4 + 15 · 7 / 4 =
= 15/4 · (√7 + 7)

-
Автор:
soto - 6 лет назад
-
0
-
-
Добавить свой ответ
-
подберите антоним к слову живот,встречающемуся в выражениях: живота не жалеть,живот положить.укажите значения этих фразеологизмов
-
Предмет:
Русский язык -
Автор:
raison7laa - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
напишите пожалуйста текст отзыв или рецензию на художественный текст Людмилой Улицкой " Восковая уточка":охарактеризуйте тему,жанр,сюжет,героев,композицию,стиль,художественную идею,образ повествователя;определите авторскую позицую,а также выразить своё отношение к прочитанному.
-
Предмет:
Литература -
Автор:
serrano - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
Найдите все натуральные значения X ,при которых верно неравенство: х/8 <3 1/48
-
Предмет:
Математика -
Автор:
rice - 6 лет назад
-
Ответов:
0 -
Смотреть
-
-
сочинение на тему "Хочу сказать спасибо"
-
Предмет:
Литература -
Автор:
hans2voa - 6 лет назад
-
Ответов:
1 -
Смотреть
-
