Из точки О, лежащей вне двух

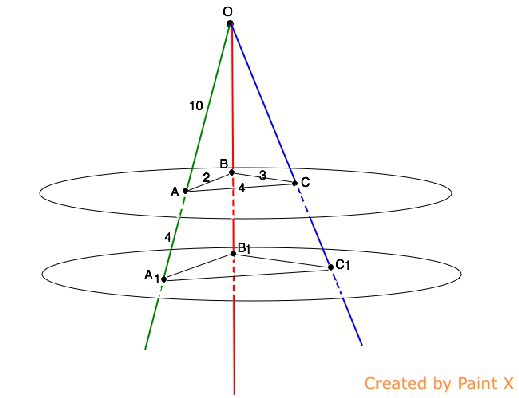
Из точки О, лежащей вне двух параллельных плоскостей альфа и бета, проведены три луча, пересекающие плоскости альфа и бета соответственно в точках А, В, С и А1, В1, С1. (ОА < ОА1). Найдите периметр А1В1С1, если АО = 10 см, АА1 = 4см, АВ = 2 см, ВС = 3 см, АС = 4 см.

 

Я видел решение этой задачи, если можно будьте добры с рисунком.

Ясно, что из одной точки можно провести к плоскости сколько угодно лучей  как под равным, так и  под разным углом, и точки их пересечения с плоскостью могут располагаться в разных ее частях, не обязательно на одной прямой.  Сделаем рисунок. Рассмотрим ∆ А1ОВ1. Так как АВ и А1В1 расположены в параллельных плоскостях и лежат в плоскости ∆ А1ОВ1, АВ║А1В1.⇒  соответственные углы этих треугольников образованные пересечением параллельных прямых и секущей равны, и ∆ АОВ~∆ A1OB1На том же основании ВС║В1С1 и АС║А1С1⇒ ∆ АВС и ∆ А1В1С1 подобны. Из подобия следует:А1О:АО=14:10=kk=1,4⇒А1В1=2•1,4=2,8 смB1C1=3•1,4=4,2 смA1C1=4•1,4=5,6 смПериметр ∆ А1В1С1=2,8+4,2+5,6=12,6 см