-
В треугольник вписан квадрат со стороной 10 см так, что две его вершины лежат на основании, а две другие – на боковых сторонах. Вычислите основание треугольника, если высота, проведенная к основанию – 13 см.
-
Предмет:
Геометрия -
Автор:
lailahkbnd - 5 лет назад
-
Ответы 1
-
Пусть в треугольнике ABC BH - высота. MNPQ - квадрат, точка M лежит на стороне AB, точка N лежит на стороне BC, точки P и Q лежат на стороне АС.Рассмотрим треугольники АВС и :- угол АВС = углу MBN (общий угол);- угол ВАС = углу ВМN (как односторонние углы при параллельных прямых АС и МN и секущей АВ).Следовательно, треугольники подобны по двум углам и значит, стороны и высоты треугольников пропорциональны, т.е.: \frac{BE}{BD} = \frac{MN}{AC} BE = BH - EH = 13 - 10 = 3 смAC = \frac{BD*MN}{BE}= \frac{13*10}{3}=43 \frac{1}{3} см
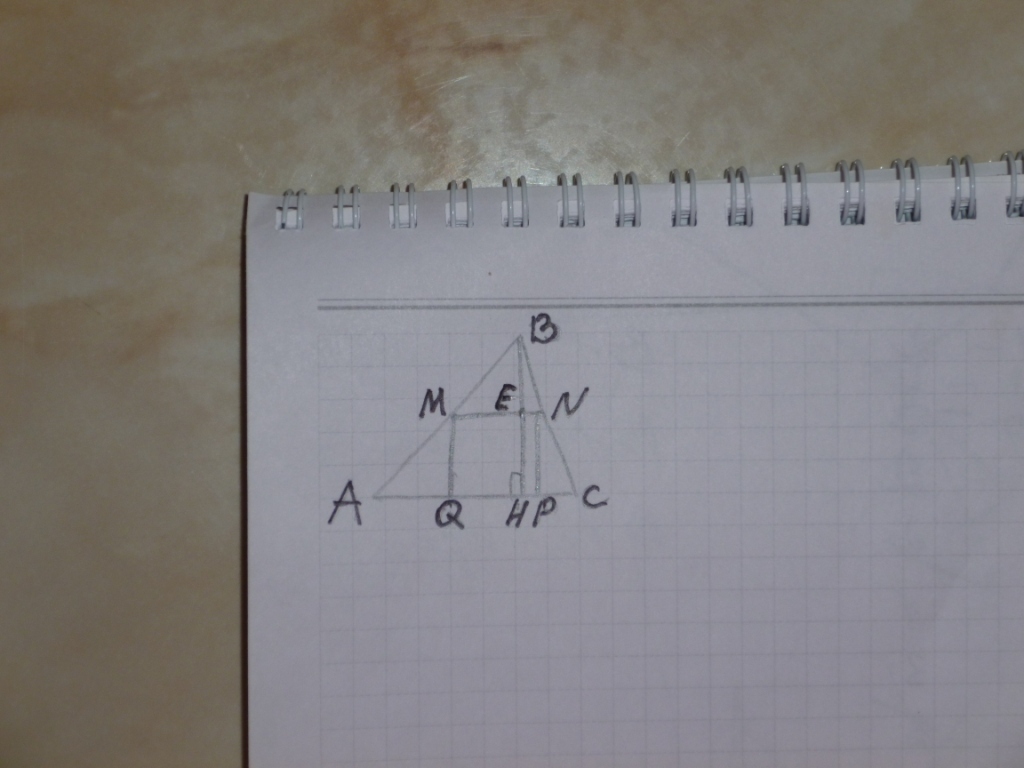
-
Автор:
peter197 - 2 года назад
-
9
-
-
Добавить свой ответ
Еще вопросы
- В чём состоит практическое значение изучения популяций? Приведите не менее 5 примеров
-
Какое положение Троекурова в обществе в романе "Дубровский?"
-
Предмет:
Литература -
Автор:
orionmorrow - 5 лет назад
-
Ответов:
1 -
Смотреть
-
-
Запишите в ответе номера верных равенств:
1) 1:2/3=2/3
2) 1,2*2/3=0,8
3)2/5+0,2=0,5
Помогите пожалуйста:)
-
Проследите по карте путь экспедиции Ф. Магеллана и назовите географические объекты, через которые он проходил
How much to ban the user?
1 hour
1 day
100 years
