-
Треугольнике ACB и BDA имеют общую основу AB, отрезки AC и BD пересекают в точке О ,известно что AC равно BD, угол ABD = угол BAC,докажите что треугольник DAO = треугольнику CBO.ОБЯЗАТЕЛЬНО ОТМЕТИТЬ ВСЁ НУЖНОЕ НА РИСУНКЕ!!
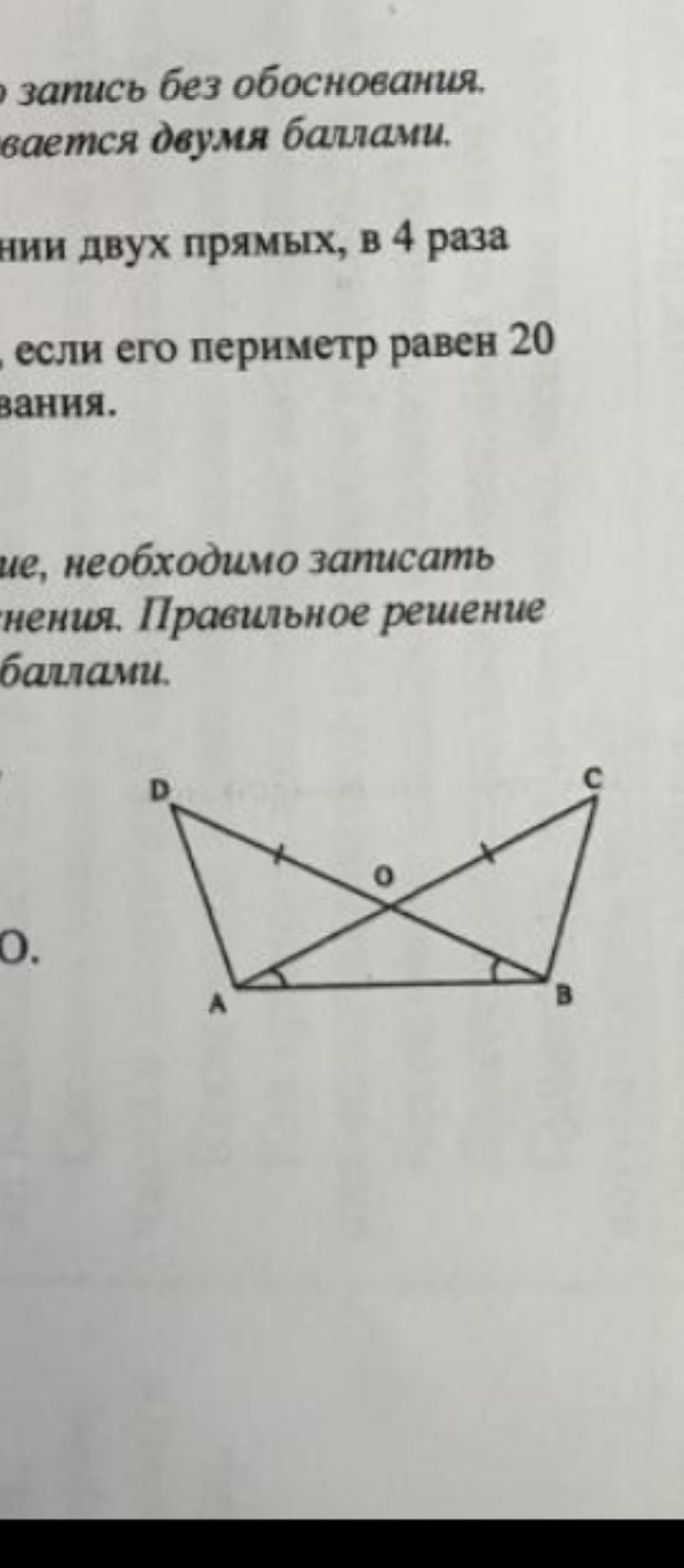
-
Предмет:
Геометрия -
Автор:
antwanrivers - 3 года назад
-
Ответы 1
-
Ответ:
Доказали, что ΔDAO = ΔCBO.
Объяснение:
Треугольники ACB и BDA имеют общую основу AB, отрезки AC и BD пересекают в точке О ,известно что AC равно BD, угол ABD = углу BAC. Докажите, что треугольник DAO = треугольнику CBO.
Дано: ΔACB и ΔBDA.
AC ∩ BD = О; AC = BD;
∠ABD = ∠BAC.
Доказать: ΔDAO = ΔCBO.
Доказательство:
1. Рассмотрим ΔACB и ΔBDA.
По условию: АВ - общая; AC = BD; ∠BAC = ∠ABD.
⇒ ΔACB и ΔBDA (по двум сторонам и углу между ними, 1 признак)
- В равных треугольниках равны соответственные элементы.
⇒ AD = BC; ∠D = ∠C.
2. Рассмотрим ΔАОВ.
∠BAC = ∠ABD (условие)
- Если в треугольнике два угла равны, то этот треугольник равнобедренный.
⇒ АО = ОВ
3. Рассмотрим ΔDAO и ΔCBO.
AD = BC; ∠D = ∠C (п.1)
OD = DB - OB
OC = AC - AO
AC = BD (условие); АО = ОВ (п.2)
⇒ OD = ОС.
ΔDAO = ΔCBO (по двум сторонам и углу между ними, 1 признак)
Что и требовалось доказать.
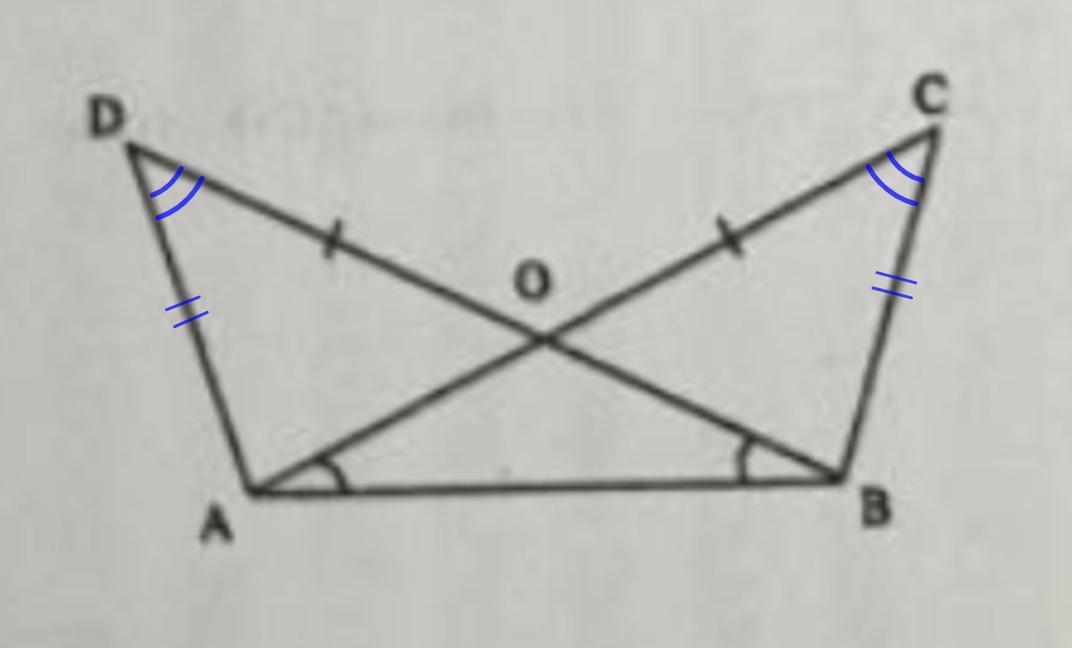
-
Автор:
abelardoj5yg - 3 года назад
-
9
-
Добавить свой ответ
-
Між учнями класу розподілили порівну 81 яблуко і 54 сливи. Скільки учнів у класі? Скільки яблук і скіль�ки слив отримав кожен учень?
-
Предмет:
Математика -
Автор:
bella43 - 3 года назад
-
Ответов:
1 -
Смотреть
-
- АВ и СD – диаметры окружности. Докажите, что хорды ВD и АС равны.
-
Марія розподілила 48 цукерок та 64 тістечка між дітьми порівну. Яка кількість дітей отримала гостинці? треба терміново!!!!!!!
-
Предмет:
Математика -
Автор:
santiago39 - 3 года назад
-
Ответов:
1 -
Смотреть
-
- В двох каністрах було 140 л води. Коли з першої каністри взяли 26л води, а з другої – 60 л води, то в першій залишилось в 2 рази більше води, ніж в другій. Скільки літрів води було в кожній каністрі?
