Помогите пожалуйста с геометрией, срочно нужен ответ

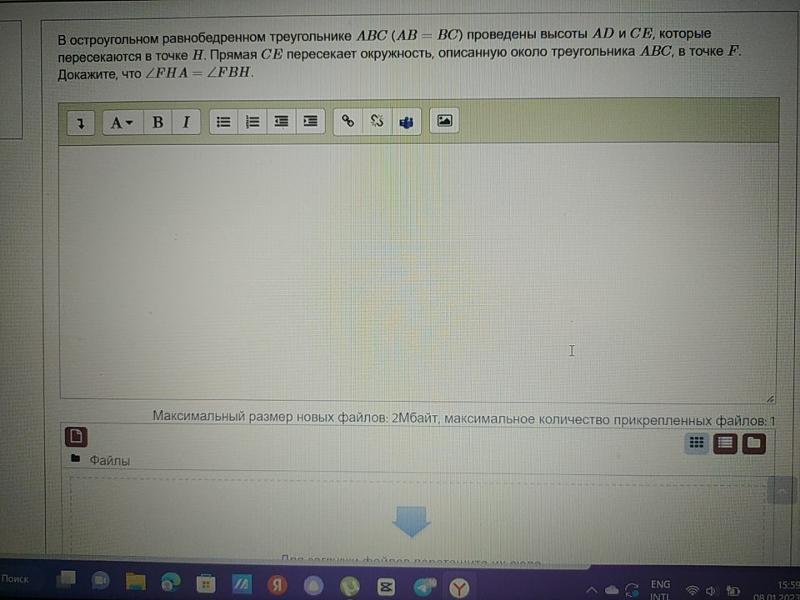
Дано: Остроугольный равнобедренный треугольник ABC (AD = BC). Высоты AD и CE пересекаются в точке N. Прямая CE пересекает окружность, описанную вблизи треугольника ABC в точке F. Чтобы доказать: FHA = FBH. Доказательство: Поскольку треугольник ADN является равнобедренным треугольником, углы NAD и NDA равны (равные стороны, противоположные равным углам). Таким образом, и ANF, и DNC являются прямыми углами, поскольку каждый угол циклического четырехугольника равен 90°. Теперь рассмотрим треугольник NBC. Мы имеем, ANF = NBC (биссектрисы угла в циклическом квадрате) итак, NBC = 90° - ANF (сумма углов треугольника) или NBC = 90° - DNC (ANF = DNC ; прямые углы) или NBC + DNC = 90° или BCE + ANC = сумма углов 90 ° треугольник) или BCE + BAH = 90° [поскольку углы ANC и BAH являются внутренними углами ∆ABC .............(1) Рассматривая треугольник AFB, мы имеем AFN = BFN (углы, разделенные одной и той же дугой на одной и той же стороне хорды), поэтому ANF = BNF ...........(2) Поскольку угол NAF = угол FBN ; прямые углы) BHF Теперь , BFH + BHF = 90°, так как внешний угол AFC равен внутреннему, противоположному ему, т.е. BHF.......(3) Добавление уравнений ‘ 1’ и ‘3’ BFH + BHF + BCE +BAH=180° .....или....FBH + FHA=180°... или....FHA = FBH {путем вычитания BFH с обеих сторон} . Следовательно, доказано.