-
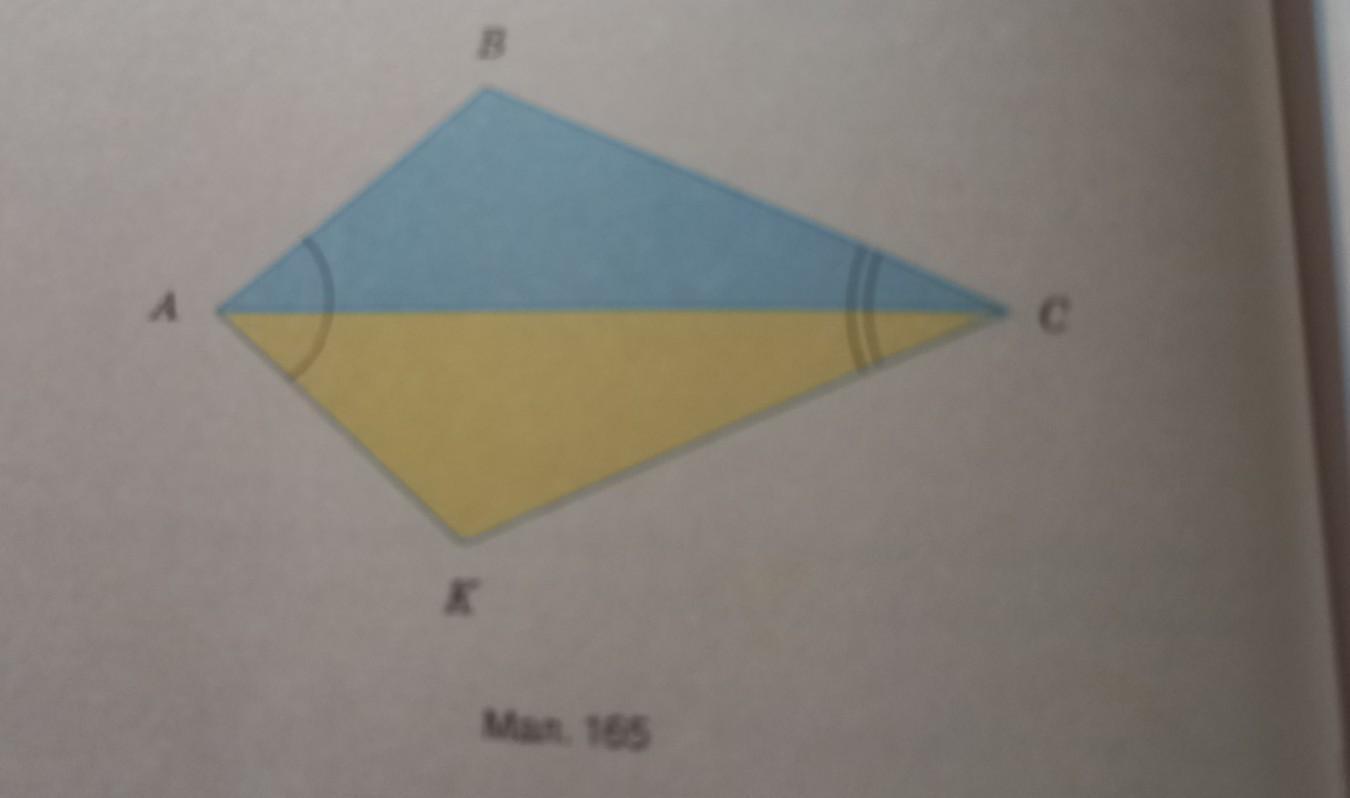
7.Зображені на малюнку 165 трикутники ABC i AKC такі,що /_BAC=/_BCA=/_KCA Доведіть,що AB=AK
Ответы 1
-
Ответ:
Враховуючи, що трикутник ABC і трикутник ABC подібні, з відповідними рівними кутами, можна показати, що їх сторони пропорційні.
Назвемо співвідношення сторін AB і AK "k". Тоді ми можемо написати:
AB / AK = BC / KC = AC / KC
Оскільки трикутники схожі, співвідношення відповідних сторін має бути рівним. Отже, ми можемо прирівняти два вирази:
AB / AK = BC / KC = AC / KC = k
Розділивши обидві сторони рівняння на AK, ми отримуємо:
AB / AK = k
А оскільки k = AB / AK, ми можемо записати:
AB = k * AK
Сенс-це просто співвідношення двох сторін, воно повинно бути безрозмірним числом. Отже, множення обох сторін рівняння на AK не змінює значення AB. Отже, AB = AK, що означає, що дві сторони рівні.
Отже, якщо трикутники ABC і JACK такі, що /_bac = /_bca = /_cca, то можна довести, що AB = AK.
Объяснение:
-
Автор:
geniekvaa - 2 года назад
-
8
-
-
Добавить свой ответ
-
Морфологія. Випишіть з рядка зайвий іменник. Вибір обгрунтуйте (поясніть). 1. НБУ, фугу, Капрі (острів), ему 2. любов, розкіш, паморозь, путь 3. яблуко, село, золото, болото дам 20балов
-
Предмет:
Українська мова -
Автор:
clark58 - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
2 Спишите предложения. Найдите односоставные предложения с главным подлежащим. Обозначьте его. Какие это предложения? членом - 1) Сильный дождь. 2) С утра в саду поют птицы. 3) Совсем тепло. 4) Первое зимнее утро. 5) От дождя всё мокро. 6) Близится вечер. 7) Прозрачный ручей. 8) Реки, озёра, океаны! 9) Земля моя - моя Земля! 10) Мелкий дождь стучит по стеклу. -көмек !!!
-
Предмет:
Русский язык -
Автор:
korin - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
62:х+38=40.........?
-
Предмет:
Математика -
Автор:
vincentbryant - 2 года назад
-
Ответов:
2 -
Смотреть
-
- ПОМОГИТЕ ПОЖАЛУЙСТА Доповнити речення: 1. Оксиген - _____________ елемент . 2. Хімічний елемент _________ утворює просту речовину озон . 3. Найбільший вміст ____________ в гірських породах і мінералах. . 4. У воді розчинений __________________. 5. Молекула кисню складається з трьох атомів кисню_______________ . 6. До складу молекули води входить _____________________. 7. Кисень відкрили _______________________. 8. У атмосфері Землі присутні ______________________ 9. __________________є головною «фабрикою» по виробництву кисню . 10. Повітря - це ___________________________. 11. В акваріумі риби дихають _______________, розчиненим у воді. 12. У повітрі найбільше за об'ємом ______________________.
