-
В ромбе ABCD с плошадью 64см², BK:KC=1:3. Найдите площадь треугольника AKC (рисунок 2).
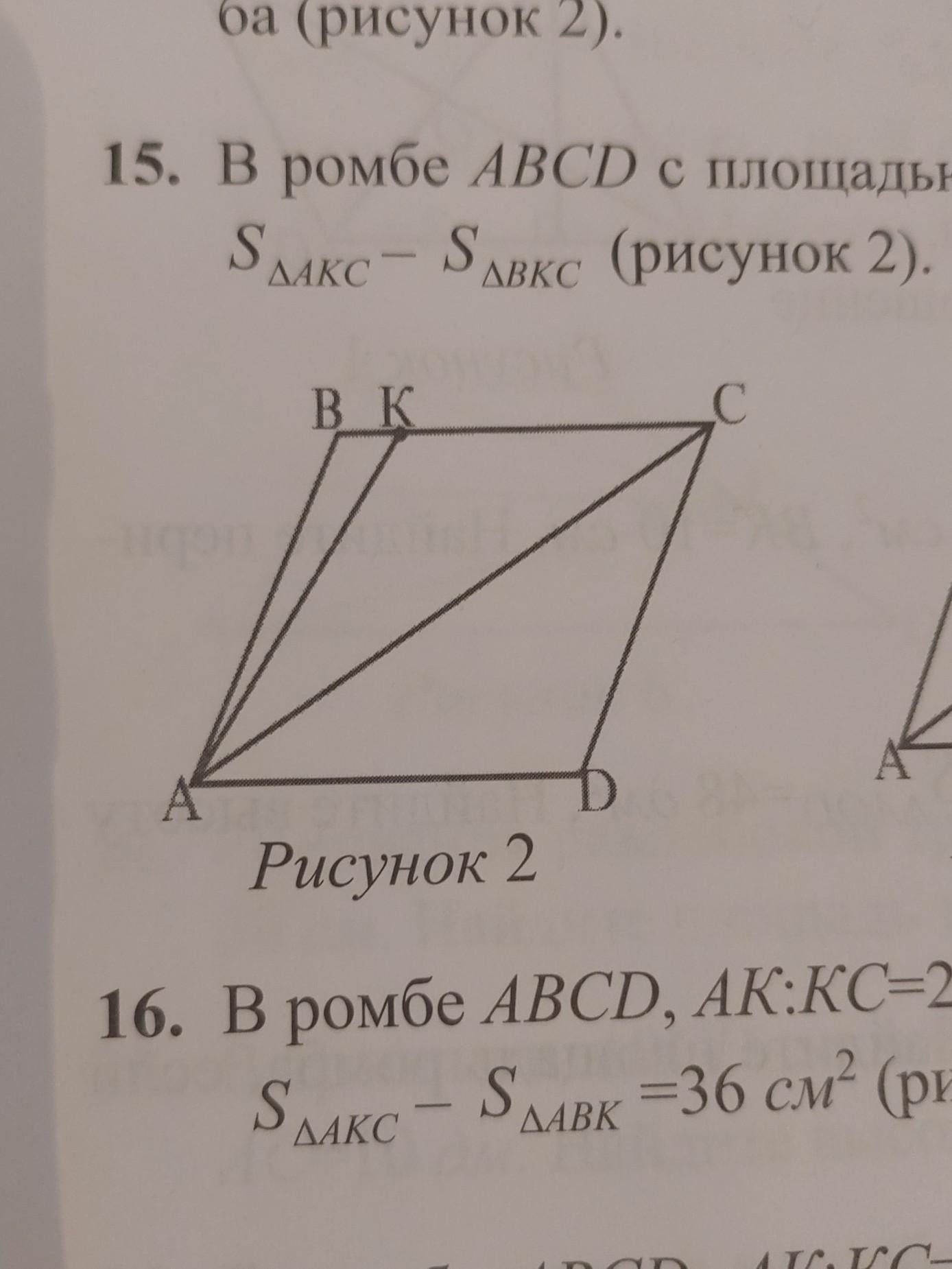
-
Предмет:
Геометрия -
Автор:
morgancarter - 2 года назад
-
Ответы 1
-
Объяснение:
Для решения задачи можно воспользоваться следующими свойствами ромба:
1. Диагонали ромба взаимно перпендикулярны и делят его на четыре равных треугольника.
2. Площадь ромба равна половине произведения диагоналей.
Пусть диагонали ромба ABCD имеют длины d1 и d2. Тогда площадь ромба равна (1/2)*d1*d2, т.е. (1/2)*d1*d2 = 64.
Так как треугольники ABK и CBK имеют равные площади и отношение BK:KC=1:3, то точка K находится на расстоянии 1/4 от диагонали AC, ближе к точке A. То есть, AK/KC=1/3 и AK=AC/4.
Из прямоугольного треугольника ABC с гипотенузой AC и катетами AB и BC следует, что AB^2 + BC^2 = AC^2. Так как AB=BC (так как ромб), то AB^2 + AB^2 = AC^2 и AB = BC = AC/√2.
Теперь можем выразить d1 и d2 через AC:
d1 = AC, d2 = AC/√2.
Подставляя d1 и d2 в уравнение (1/2)*d1*d2 = 64 и заменяя AC на 4*AK, получаем:
(1/2)*(4*AK)*(4*AK/√2) = 64
AK^2 = 8
Таким образом, площадь треугольника AKC равна (1/2)*AK*AC/2 = AK^2/2 = 4.
-
Автор:
julian890 - 2 года назад
-
10
-
-
Добавить свой ответ
-
( \frac{1}{7} \sqrt{14) {}^{2} } знайти значення виразу
-
Предмет:
Алгебра -
Автор:
honey locks - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Көп нүктенің орнына тиісті қосымшаларады қоып , жаз
-
Предмет:
Қазақ тiлi -
Автор:
daniels77 - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
Для мене уміння запобігати пропаганді і маніпулюванню – це коротко, будь ласка
-
Предмет:
Обществознание -
Автор:
davion - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
фразеологізми які мають дієслова з закінченням на но/то
-
Предмет:
Українська мова -
Автор:
schneider - 2 года назад
-
Ответов:
1 -
Смотреть
-
