В файле рисунок если что-то не понятно.Срочно, У нас есть два треугольника ABC и a1 b1 c1 по условию они подобны периметр ABC / периметр а1b1c1 = 2/3, площадь ABC / на площадь a1 b1 c1 равно 260 чему равна площадь ABC

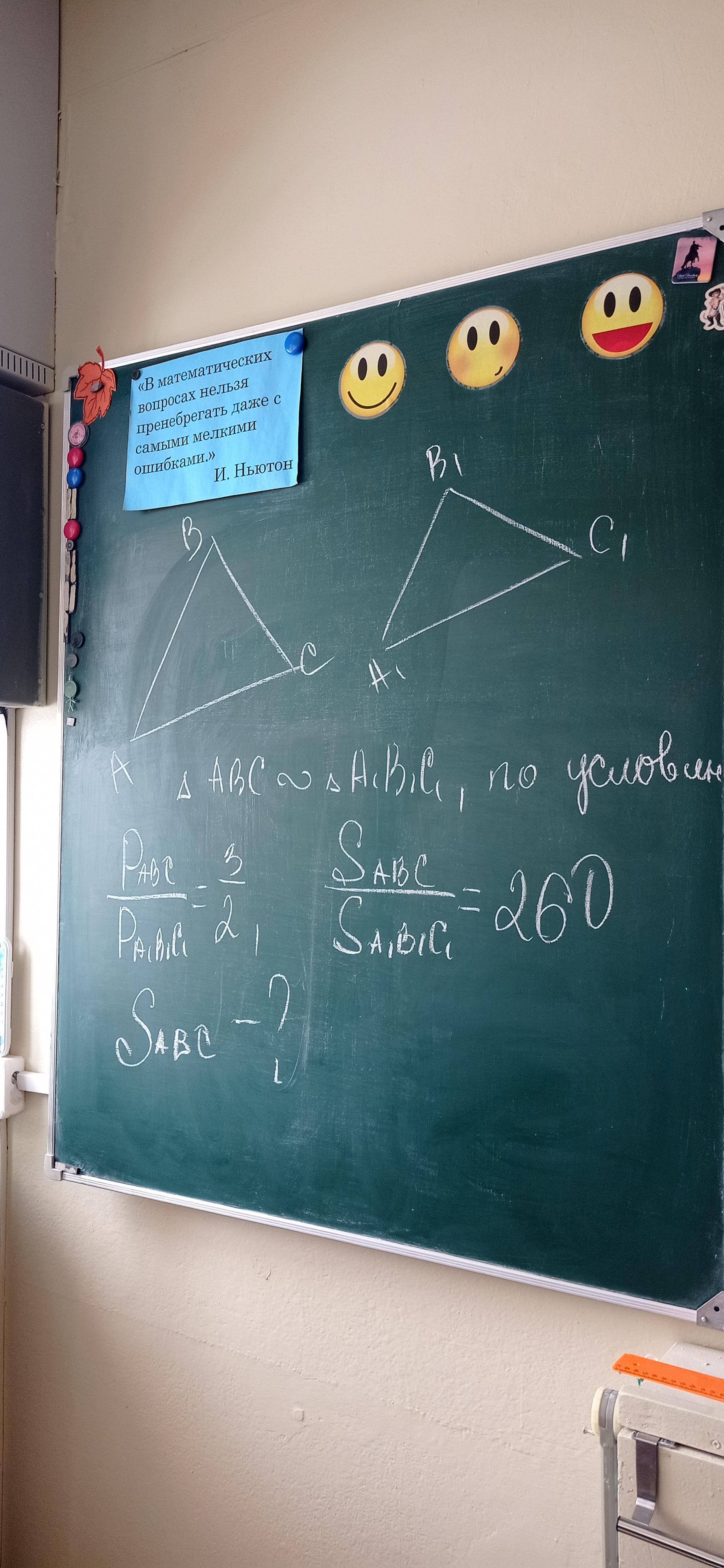
Ответ:

Якщо треугольники ABC і a1b1c1 подібні, то вони мають спільні кути і сторони в однакових пропорціях. Отже, відношення сторінок треугольників ABC і a1b1c1 є рівним відношенню їх периметрів:

Периметр ABC / Периметр a1b1c1 = 2/3

Це можна переписати як:

(AB + BC + AC) / (a1b1 + b1c1 + c1a1) = 2/3

Якщо треугольники ABC і a1b1c1 подібні, то відношення їх площі також є рівним відношенню квадратів відповідних сторінок:

Площа ABC / Площа a1b1c1 = (AB^2 + BC^2 + AC^2) / (a1b1^2 + b1c1^2 + c1a1^2)

За умовою задачі це відношення дорівнює 260. Також ми знаємо, що відношення периметрів дорівнює 2/3, тому ми можемо виразити одну зі сторін ABC через сторони a1b1c1. Наприклад, якщо ми виразимо AB через a1b1, b1c1 та c1a1, випустимо:

AB = (2/3) * (a1b1 + b1c1 + c1a1) * (a1b1 / (a1 + b1 + c1))

Тепер ми можемо виразити площу ABC через сторони a1b1c1 та відомо відношення площі:

Площа ABC = 260 * (a1b1^2 + b1c1^2 + c1a1^2) / (AB^2 + BC^2 + AC^2)

Підставивши значення AB, BC та AC, виберемо:

Площа ABC = 260 * (a1b1^2 + b1c1^2 + c1a1^2) / [(2/3)^2 * (a1b1 + b1c1 + c1a1)^2 * (a1b1^2 / (a1 + b1 + c1) ^2 + b1c1^2 / (b1 + c1 + a1)^2 + c1a1^2 / (c1 + a1 + b1)^2)]

Отже, за відомими відношеннями сторінка та площа, ми можемо

Объяснение: