-
У кута AKD, вписано коло, яке дотикається його сторін у точках С, Е, F. Знайдіть Р кута AKD, якщо АС, + КЕ + DF =14смПомогите срочно даю лудший ответ и 100балов
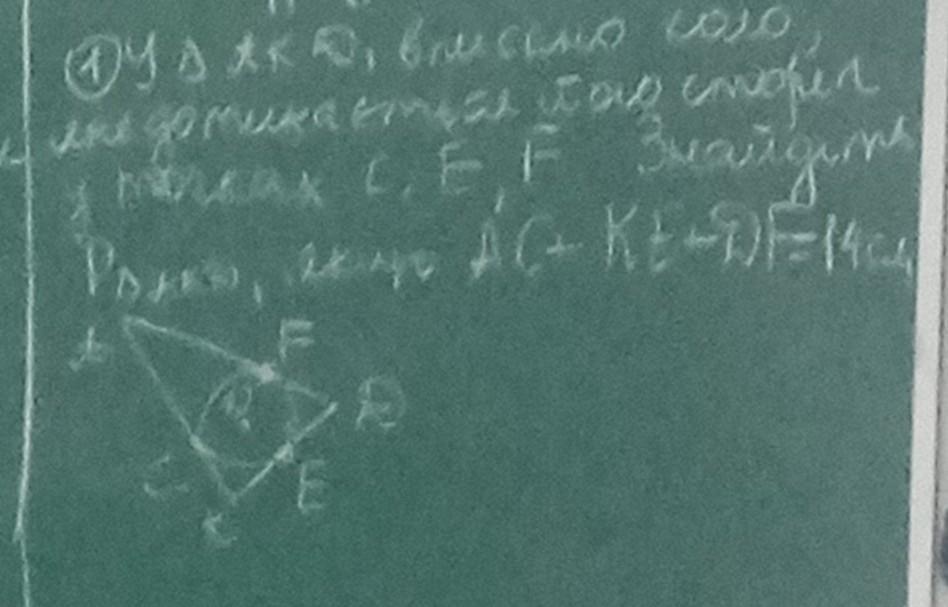
Ответы 1
-
За теоремою про вписані кути, маємо, що кут АСК = КЕF, АКЕ = СFD, а кут AKD дорівнює половині кута між хордами СК та DF, тобто:
P(AKD) = 1/2 * P(CSF)
Позначимо радіус вписаного кола як r. Оскільки С, Е та F дотикаються до кола, то вони розташовані на відстані r від середини відрізку КД. Таким чином, КЕ + СD + DF = 2r, але за умовою КЕ + СD + DF = 14см.
Тоді 2r = 14см, тобто r = 7см.
Також за теоремою про трикутники з дотичними, маємо, що:
АК = АС = АЕ
ДК = DF = CF
Отже, АК + КД = АС + СD + ДК + КЕ + ЕА + АЕ = 2r + 2АК, тобто:
3АК + КД = 14см + 2r = 28см
Також можна записати, що:
sin(P(AKD)) = CF / АК = DF / АК
sin(P(CSF)) = KE / АК = CD / АК
Звідси маємо:
sin(P(AKD)) / sin(P(CSF)) = DF / CD
Але оскільки СФ паралельно АЕ, то СD = DF, тому:
sin(P(AKD)) / sin(P(CSF)) = 1
З цього випливає, що P(AKD) = P(CSF). Таким чином:
P(AKD) = 1/2 * P(CSF) = 1/2 * 180° = 90°
Отже, Р кута AKD дорівнює 90°.
-
Автор:
roseokan - 2 года назад
-
7
-
-
Добавить свой ответ
-
привет на українськом?
-
Предмет:
Українська мова -
Автор:
elisabethvelasquez - 2 года назад
-
Ответов:
1 -
Смотреть
-
-
бабуся спекла 18 пиріжків з яблуками що становить 3/7 кількості пиріжків з вишнями.а з сиром 2/7 кількості пиріжків з вишнями. СКІЛЬКИ ВСЬОГО СПЕКЛА ПИРІЖКІВ БАБУСЯ?
запишіть розв'язання та відповідь ХЕЕЛП
-
Предмет:
Математика -
Автор:
diamondayala - 2 года назад
-
Ответов:
2 -
Смотреть
-
-
Як вивчить вірш на пам'ять скажіть пж
-
Предмет:
Українська література -
Автор:
jakayla - 2 года назад
-
Ответов:
2 -
Смотреть
-
-
ХАЛЯВНЫЕ БАЛЛЫ!(100)
2+2=?
-
Предмет:
Математика -
Автор:
dayami - 2 года назад
-
Ответов:
2 -
Смотреть
-
